Monthly Archives: April 2014

Lever Classes

,

The lever is one of the six simple machines.* It takes an input force and multiples it (by a factor known as the mechanical advantage) to create a larger output force.

Levers do not violate the conservation of energy because the input force has to be applied over a longer distance than the output force is applied over. (For example, a five newton force applied over one metre can produce a five hundred newton force over one centimetre; in both cases the work done is five joules.)

The operation of a lever is accomplished through the use of a rigid bar (the lever) and a fulcrum, or pivot. All levers can be placed into one of three classes depending of where the input force (red in the diagrams below), and output force (blue in the diagrams below) are applied relative to the fulcrum.

Class 1

Examples: crowbar, scissors, pliers

lever-class1

A class one lever is the type most familiar to people, and is often compared to a seesaw. The output force and the fulcrum are usually very close together, giving a very large mechanical advantage, as in the case of a crowbar, which typically has a mechanical advantage of six or more.

Class 2

Examples: wheelbarrow, nutcrackers, bottle opener

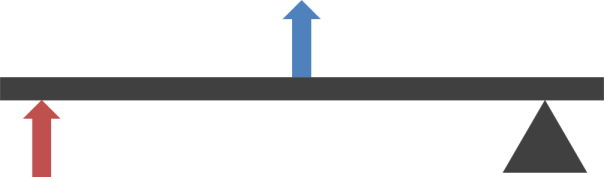
lever-class2

Class 2 levers are less familiar; many people using  a class 2 lever will not have realised that are using a lever at all. A class 2 lever typically has a mechanical advantage of two or three.

Class 3

Examples: tweezers, tongs, human jaw

lever-class3

Class 3 levers have a mechanical advantage of less than one, meaning that the output force is lower than the input force, and they are therefore not very common. They are only used when a force is required to be applied at a distance, as in the case of barbeque tongs or tweezers; or when using a class two lever would be impossible, as in the case of the human jaw (the jaw muscles would have to be in front of the teeth).

* The other five simple machines are the wheel & axle, the pulley, the inclined plane (i.e. the ramp), the wedge, and the screw.

Types of Dam

,

A dam is a feature built to hold back water. They come in a number of different types.

Perhaps the most well-known type of dam is the arch dam, which holds back water in much the same way as an arch holds up a building – by distributing force perpendicularly. In the case of an arch dam, the forward force of the water is distributed sideways into the surrounding abutments (i.e. the “walls” on either side of the dam).

hoover-dam

The Hoover Dam, a concrete arch-gravity dam.

Gravity dams hold back water by simply being too big and heavy for the water to move. Gravity dams are often combined with arch dams to create arch-gravity dams.

wanapum-dam

The Wanapum Dam, an earth-filled gravity dam.

Gravity dams come in many types: mass concrete dams, which are exactly what they sound like – big lumps of concrete; hollow concrete dams, which are also exactly what they sound like; buttress dams, which are hollow dams that are supported by angled buttresses that are driven into the ground by the force of the water behind them; and embankment dams which are created by piling up and compacting soil, sand, clay or rock.

buttress-dam

The Barrage de Roselend, a concrete buttress dam.

embankment-dam

The Mica Dam, an earth-filled buttress dam, and the fifteenth tallest dam in the world.

 A barrage is a special type of dam that is not designed to create a reservoir, like other dams, but rather to regulate the amount of water flowing along a river.

barrage-dam

The Pioneer River barrage, which regulates water flow along the Pioneer river.

Barrages consist of a number of gates in between supporting piers that can be opened and closed as required. I had originally decided that the Thames Barrier was a barrage, but now I think it’s more of a temporary dam than a barrage: I think that the head (the difference in height either side of the dam) when the Thames Barrier is in use is too large for it to be considered a barrage.

Pylon Turns and Long Line Loitering

,

A pylon turn is a manoeuvre in which an aeroplane flies in a circle, banked with one wing pointed towards a fixed point on the ground.

Pylon turns were originally used in air racing, and are used extensively by military aircraft, as it allows them to easily and accurately direct fire onto targets on the ground for a long period of time.

ac-130-pylon-turn

In the photograph above an AC-130 Spectre gunship is executing a pylon turn. The aircraft’s GAU-2/A miniguns and L/60 Bofors cannon are visible on the aircraft’s left-hand side, pointing towards the centre of the pylon turn.

pylon-turn

An AC-47 Spooky gunship executing a pylon turn whilst directing tracer fire against a target on the ground.

The physics of a pylon turn depend on the bank angle, the speed of the aircraft and the aircraft’s altitude, but these are intrinsically linked. You can pick two, but the third is then fixed: a pylon turn can only occur at a certain bank angle for a given speed and altitude; or at a certain speed for a given bank angle and altitude; or at a certain altitude for a given bank angle and speed.

A pylon turn also allows for a procedure called long-line loitering, in which a container can be lowered to the ground from a moving aircraft, remaining stationary on the ground in the process. This enables delivery and retrieval of material without the aircraft having to land.

long-line-loiter-patent

Patent drawings from US patent US3724817 A. Click to enlarge.

A drag cone (a small parachute) helps to pull the line into a loop, keeping it relatively stationary and allowing the far end of the line to drop to the ground. This technique has been used to retrieve personnel and even to deliver mail.

 

Real and Apparent Weightlessness

,

The strength of the gravitational field at Earth’s surface g is 9.81 newtons per kilogram. This means that every kilogram of mass feels a force of 9.81 newtons pulling it downwards towards the centre of Earth.

As you climb higher and higher, the value of g becomes smaller and smaller. At the peak of Mount Everest, g?=?9.79?N/kg, and at the summit of Chimborazo, the farthest point from Earth’s centre, g?=?9.78?N/kg.

So what is the value of g aboard the International Space Station, in orbit around Earth? You would be forgiven for thinking that the answer is 0?N/kg, because the environment the astronauts are in is often described as “zero-g”, but this is not the case. The value of g aboard the ISS is actually 8.65?N/kg, only 12% less than on Earth’s surface.

zero-g-appleAn apple floats in mid-air aboard the ISS.

The astronauts aboard the ISS experience apparent weightlessness, not true weightlessness. The reason they appear to be in a zero-g environment is only because they are in orbit around the Earth – if the ISS were to slow to a halt it would fall towards Earth just like an object on Earth’s surface (though it’d fall a little bit slower at first).

In orbit the ISS is falling towards Earth at just the same rate as Earth is curving away, keeping it at a constant distance from Earth’s surface.* Because astronauts are in constant freefall they don’t push against the “floor” and the “floor” doesn’t push against them and therefore they feel weightless. If you’ve ever felt a little bit lighter in a lift as it started to move downwards, just imagine that effect taken to an extreme in a lift shaft where you can never hit the bottom.

g-with-height

Even geostationary satellites, like those that supply satellite TV, at a distance of 36000 km from Earth aren’t in zero-g. If they weren’t within Earth’s gravitational field they wouldn’t orbit and would fly off into space; for geostationary satellites g?=?0.224?N/kg.

The closest human beings have ever been to true zero-g is on the way to the Moon, at the point at which the gravitational pull of the Earth in one direction was equal to the gravitational pull of the Moon in the other direction. Because the mass of the Moon is about 1/81 of the mass of the Earth and the strength of a body’s gravitational field depends on the square of the distance from the body this point is about nine-tenths of the distance between the two: 346?000 km from Earth. At this point the pull from the Earth is 0.0032?g and the pull from the Moon is the same, but in the other direction.

* Imagine a giant cannon firing horizontally: too slow and the cannon ball will hit the ground, too quick and the cannon ball will fly off into space. But if the cannon fires at just the right speed the cannon ball will drop towards the ground at just the same rate as the ground curves away.

The Beaufort Scale

,

Many of you will be familiar with the Beaufort Scale, used to measure wind speed. (Although it’s full name is the Beaufort Wind Force Scale, it does not measure force in the physical sense.) Although the scale is usually taken to relate to open ocean conditions (e.g. Force 6 has been referred to as “Strong Breeze – Long waves begin to form. White foam crests are very frequent. Some airborne spray is present.”) there is an empirical relationship between Beaufort Scale and wind speed:

v = 0.836 B^{3/2}

Where v is windspeed and B is the 1946 Beaufort Scale.

beaufort

The Beaufort Scale only officially goes up to Force 12 (“Hurricane Force – Huge waves. Sea is completely white with foam and spray. Air is filled with driving spray, greatly reducing visibility.”) but it could be (and has been) applied to hurricanes (normally measured on the Saffir-Simpson Scale), or tornadoes (normally measured on the Enhanced Fujita Scale). Hurricane Felix, a Category 5 hurricane that struck Nicaragua and Honduras in 2007 had a peak wind speed of 175 mph, equivalent to a Beaufort Scale of 20.7; and the 318 mph wind speed measured by Doppler radar during the Moore Tornado of 1999 would be equivalent to a Beaufort Scale of 30.7.