Tag Archives: optics

Depth perception in jumping spiders

,

The vast majority of animals judge distance by using binocular (two-eyed) stereoscopic vision; other animals use accommodation (how much the animal has to adjust focus) and motion parallax (how much the image moves across the retina). But a new paper* shows that at least one animal, a jumping spider known as Hasarius adansoni, perceives depth by using image defocus, comparing a defocused image from one sensor with a focused image from another sensor.

spider-retina

A horizontal cross-section of the spider retina, showing the different photoreceptive layers at different depths within the retina.

The researchers investigating the spider’s eye showed that their hypothesis about depth perception was correct with a very neat experiment. They used different colours of light, which are refracted by the spider’s eye by different amounts and therefore have different focal lengths and took video of the spider’s jumping attack. Under green light, which is detected by the L1 and L2 layers indicated above the spiders were able to accurately judge the distance to their prey, but under red light, which is not detected by the L1/L2 layers the spiders jumped short (as red light has a shorter wavelength than green). This showed that the spider was judging distance by comparing a defocused image on L2 with a focused image on L1; under red light the spider receives incorrect information about the amount of defocusing required and therefore doesn’t attack correctly.

* Takashi Nagata et al, “Depth Perception from Image Defocus in a Jumping Spider”, Science 335 (2012): 469-471. doi: 10.1126/science.1211667.

Demonstrating refractive index

, ,

The refractive index of a material governs how much light bends as the light moves into it. You’ve probably seen this bending effect when looking at the surface of a swimming pool: the bottom of the pool looks closer to the surface than it actually is because light rays bend as they travel from water to air.

But if the refractive index of two materials is the same, as is the case for sunflower oil and Pyrex, then light doesn’t bend at all, and you end up with the nice effect demonstrated below.

To say that this demonstration impressed my pupils would be an understatement.

My favourite photograph from the 2012 Olympics

, , ,

During the 2012 Olympics, the underwater cameras in the swimming pool have been tweeting regularly. On Sunday, the PoolCam sent out my favourite image of the whole London 2012 Olympic Games: a magnificent demonstration of total internal reflection.

Light refracts as it travels from one medium to another. Total internal reflection occurs when light travels from a medium with a high refractive index to one with a low refractive index at an angle above the critical angle for those two media.

In the photograph above you can see out of the pool at the top of the image because the angle of incidence is less than the critical angle. Beyond the critical angle, light is totally internally reflected and the bottom of the pool is reflected back towards the camera. Because the angle is the same in all directions this creates a semicircle, which is visible at the top of the image.

If the camera is on the bottom of the pool looking up you therefore see a perfect “see-through” circle looking at the roof, surrounded by water reflecting the bottom of the pool. This effect can be seen in a previous @L2012PoolCam photograph:

What is a ‘Retina’ display?

, , ,

Apple describes some of its products as featuring a “Retina” display. But what does that actually mean?

The individual pixels (each one made up of three red, green and blue subpixels) that make up my laptop’s display, viewed through a magnifier.

The main claim that Apple makes of its Retina display is that the pixels used are so small that they are too small to be seen individually by the human eye. In physics terms, this means that these pixels are below the resolving power of the human eye.

The resolving power of the human eye is about 60 arcseconds, or 0.0167 degrees. This means that any two objects separated by an angle smaller than this will appear as one object to the eye. The minimum vertical or horizontal spacing between two items which are visible as separate items is therefore given by dtan(θ) where d is the distance to the items and θ is the resolving power of the eye.

Assuming that the display in question is held or viewed at a distance of 30 cm from the eye, this distance is found to be 0.0873 millimetres. This means that a person with normal vision will be able to discern individual pixels on any display with fewer than 11.5 pixels per millimetre.

As can be seen from the graph above, the screen of the iPhone 4 does possess a greater density of pixels than the human eye can perceive; but the iPad 3 and the just-released 2012 MacBook Pro do not. (None of this matters of course, because “Retina” is just a trademark that Apple uses as a marketing term.)

An argument could be made, in the case of the MacBook Pro, that the distance between the screen and the eye would usually be larger than 30 cm. If the distance was 50 cm that would make the resolution of the eye 6.88 pixels per millimetre and therefore give the 2012 MacBook Pro a “true” retina display.

Arbitrage at the speed of light

, , , ,

arb·it·rage n /ˈɑrbɨtrɑːʒ/
the practice of taking advantage of a price difference between two or more markets.

The image most people have of stock markets is of men (and it is always men) in suits using hand signals and shouted verbal commands to buy and sell stocks and shares; this system is called “open outcry” and in reality is used only very rarely.

The vast majority of trading now takes place via computer, and this has altered the way in which markets operate. Not only are traders using computers, but now the traders are computers, operating at very high speeds to execute pre-programmed trading strategies.

As computer hardware and software have improved it is no longer the speed at which computers operate that is most important, but rather the time taken for light to travel down the optical fibre between trading locations. Typical trading latencies are now below five hundred microseconds, enabling traders to make more than two thousand trades per second.*

Because the speed of light has become the limiting factor the physical location of trading offices is becoming more and more important. Well-positioned traders (if you’ll excuse the pun) can take advantage of the difference in price between two markets – buying low in one market and selling high in another – for a profit.

For example: imagine three traders buying and selling aluminium on the London Metals Exchange through the LMEselect electronic trading system. One trader is located in London, one in Dubai (5500km from London) and the other in Singapore (10800km from London). The speed of light in an optical fibre is about 200 million metres per second so any change in price reaches the London trader almost immediately but takes 28 milliseconds to reach Dubai and 54 milliseconds to reach Singapore. The trader in Dubai has an extra 26 milliseconds to act – enough time for more than fifty 500 microsecond trades – before the information reaches Singapore. If the trader in Dubai is trading metals in both London and Singapore then it becomes possible to buy low in London and sell high in Singapore before price information can pass between the two.

In a recent paper†, academics Alexander Wissner-Gross and Cameron Freer show that “there exist optimal locations from which to coordinate the statistical arbitrage of spacelike separated securities” and plot these locations on a map.


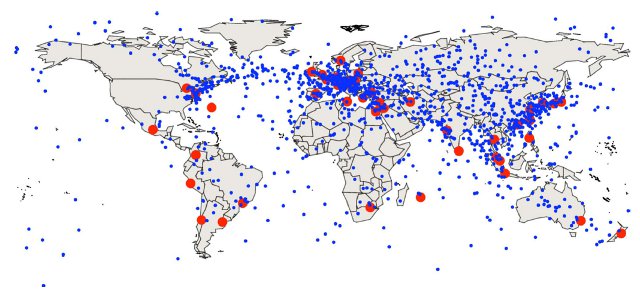
The red dots represent exchanges, the blue dots the optimal location of trading nodes between each pair of exchanges.

As the authors point out:

“[W]hile some nodes are in regions with dense fibre-optic networks, many others are in the ocean or other sparsely connected regions, perhaps ultimately motivating the deployment of low-latency trading infrastructure at such remote but well-positioned locations.”

This suggests that the location of exchanges and the speed of light may become the deciding factors as to where trading offices are sited.

* See, for example, Tara Bhupathi. 2010. “Technology’s Latest Market Manipulator? High Frequency Trading: the Strategies, Tools, Risks, and Responses”, North Carolina Journal of Law & Technology 11(2): 377-400.

† Alexander Wissner-Gross and Cameron Freer. 2010. “Relativistic Statistical Arbitrage”. Physical Review E 82(5): 056104-056110. doi:10.1103/PhysRevE.82.056104