If someone says something is “very radioactive”, what do they actually mean? How do you measure “radioactiveness”? There are many terms used in physics to describe radioactive decay and each has a specific use.
(Throughout this post I’ll be using polonium-210 as an example. Polonium-210 is most famous as the radioactive poison used to murder Russian dissident Alexander Litvinenko.)
The activity of a radioactivity substance is the number of decays that it undergoes per second: one becquerel (Bq) is one decay per second. Polonium-210 has an activity of 166 terabecquerels per gram (166 TBq/g) which means that each gram of Po-210 undergoes 166 trillion decays per second. But knowing how many radioactive decays a substance undergoes isn’t going to tell us how dangerous it is. Standing one kilometre away from a 1 TBq source is very different to standing one metre away from a 1 TBq source.
The absorbed dose, measured in grays* (Gy), is a measure of the amount of energy deposited by a radioactive source into each kilogram of mass (one gray is one joule per kilogram).
Every time a Po-210 nucleus decays it emits a particle with an energy of 5.3 MeV, which is equivalent to 8.50×10−13 joules. 1 gram of polonium-210, emitting 166 trillion of these particles per second is equivalent to 141 watts, easily enough to run a laptop or two standard 60 W lightbulbs. After a day one one-thousandth of a gram of polonium-210 would have released 12 200 joules of energy, about the same amount of energy as a twenty-five kilogram mass travelling at 70 mph. This 12 200 joules, divided evenly amongst the mass of an 80 kg human being would be more than 150 Gy, where anything more than 5 Gy at any one time is usually fatal.
Absorbed dose isn’t perfect for measuring the danger posed by a radioactive source as it doesn’t take into account where the radiation is absorbed, nor the type of radiation.
The equivalent dose only takes into account the organ or tissue being affected but the effective dose, measured in sieverts† (Sv) is designed to compensate for these failings and attempts to reflect the biological rather than the physical effects of radiation. It is calculated by combining the absorbed dose and two dimensionless factors: one to account for the type of radiation and one to account for the organ or tissue being irradiated. These factors, Q and N, combined together are called the radiation weighting factor.
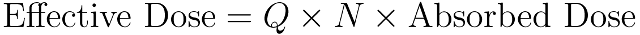
Q (sometimes called the quality factor) accounts for the type of radiation being absorbed. It is equal to 1.0 for all photons, electrons, positrons and muons; 2.0 for protons and pions; 5.0 to 20 for neutrons according to their energy; and 20 for alpha particles and the heavier products of nuclear fission. N accounts for the tissue or organ that is being irradiated. N is greatest for bone marrow, the colon, the lungs, heart or stomach; and lowest for the skin.
Looking back at the 150 Gy absorbed dose for one milligram of Po-210 we end up with a table that looks like this:
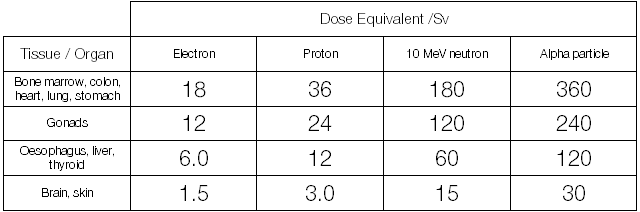150 Gy of alpha radiation incident upon the lungs or stomach (360 Sv) is approximately 250 times more damaging biologically than 150 Gy of electron or positron radiation received to the skin (1.5 Sv). For comparison, the average dose for a resident of the UK, due to natural background sources is about 2.6 millisieverts and a dose of more than 3 Sv kills fifty percent of people within thirty days.
* The gray is named after Hal Gray, a British physicist who created the field of radiobiology.
† The sievert is named after Rolf Maximilian Sievert, a Swedish medical physicist who studied the biological effects of radiation.
.
