Tag Archives: mathematics

One Million Hats

,

From the always-excellent Futility Closet, a problem by Paul J. Nahin:

Each of a million people puts his or her hat into a very large box. Each hat has its owner’s name on it. The box is given a good shaking, and then each person, one after another, randomly draws a hat out of the box. What is the probability that at least one person gets their own hat back?

Most people might think that the chance is very, very small, but it’s not. It’s actually more than 60%. How can this be true?

We can view this problem as having only two possible solutions (events): either nobody gets their hat back, or at least one person gets their hat back. The sum of the probabilities of these events must be equal to one and therefore if we can work out the probability that nobody gets their own hat back, then the probability that at least one person does is one minus that.

For each person, there is only a one-in-a-million chance that they have picked their own hat, and thus a 999999 in 1000000 chance that they have not got their own hat.

\Pr \left( \textnormal{one incorrect hat} \right) = \frac{999999}{1000000}

\Pr \left( \textnormal{one million incorrect hats} \right) = \left( \frac{999999}{1000000} \right)^{1000000}

\Pr \left( \textnormal{one million incorrect hats} \right) = 0.368

If the probability of all one million people picking the incorrect hat in 0.368, then via our previous reasoning, the probability of at least one person picking the correct hat is 1-0.368, or 63.2%.

This is a very counterintuitive result, but the wording of the question is key. If we changed the wording to exactly one person getting their hat back then our answer changes dramatically. Starting with our 63.2% chance, we would have to subtract the chance of two people getting their hats back, and of three people getting their hats back, and so on … until we reached the very small chance of one person, and one person only, getting their hat back.

Fixed Area, Infinite Perimeter

,

The Koch Snowflake (named after its inventor, the Swedish mathematician Helge von Koch) is a fractal with a number of interesting properties.

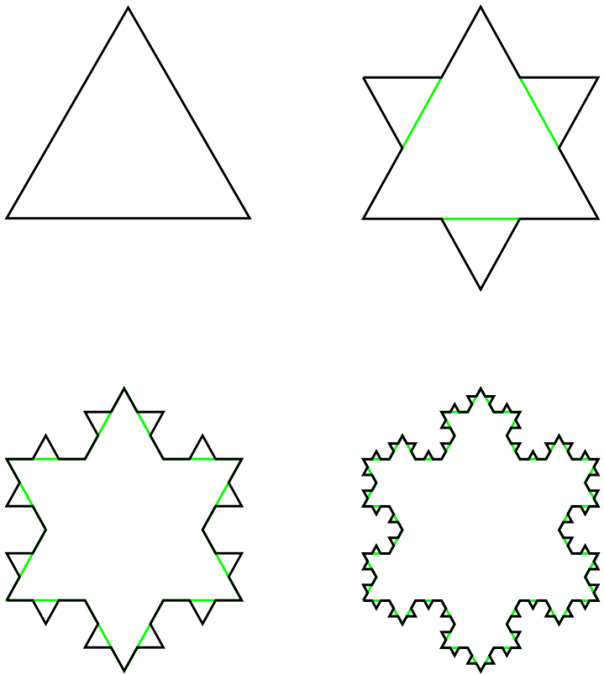
koch-snowflake-four-generations

The first four generations of the Koch Snowflake

As the number of generations increases, the area of the snowflake increases, but it increases towards a limit: eight-fifths of the size of the first (triangular) generation. This is because each additional generation adds three triangles which are one-ninth the size of the triangle added in the previous generation (for a total increase of one-third), and the additional of increasingly small triangles has a lesser and lesser effect on the overall area as the number of generations increases.

But as the number of generations increases, the perimeter of the shape continues to grow, without approaching a limit: each generation of the Snowflake has a perimeter which is four-thirds of the previous generation’s perimeter. This is because the additional perimeter added each time is four times one-third of the length of each side, for a total increase of four-thirds, as opposed to the one-third increase in area. Because four-thirds is greater than one, the perimeter tends to infinity, whereas the area (which at one-third is less than one) does not.

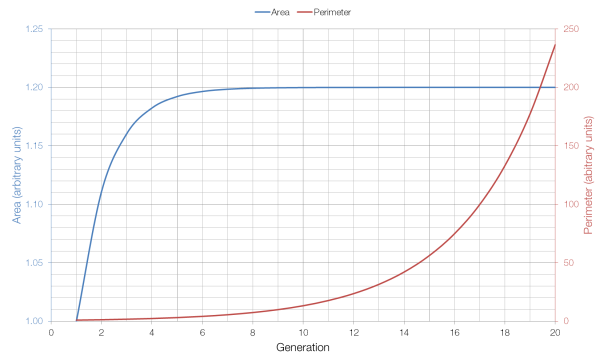
koch-snowflake-graph

As you can see from the graph above, the area approaches its limit very quickly, whereas the perimeter grows very quickly (which is why it has to be shown on a different axis).

Dot Product and Cross Product

There is more than one way to multiply two numbers together.

Normal everyday multiplication (e.g. 3 \times 4 = 12) isn’t always good enough for physics. If we want to multiply two vectors (quantities that have both size and direction) like force or velocity, then the direction of those vectors matters. The result of a 3 N force multiplied by a 4 N force will depend on their relative directions: if they are pointing in the same direction we will get a different answer to if they are at right angles to each other.

When multiplying two vectors, physicists use one of two products: the dot product or the cross product. Both the moment of a force (the torque) and the work done by a force are calculated by finding the product of a force and a distance, but calculating work done uses the dot product and calculating the moment of a force uses the cross product.

The dot product yields a scalar answer, an answer that does not have a direction. Work done is a scalar quantity, and doesn’t have a direction, hence the use of the dot product. The cross product yields a vector answer, which does have a direction (if you’ve ever used Fleming’s Left Hand rule to find the force acting on a current-carrying wire in a magnetic field you’ve found the cross product of those two vectors). The moment of a force does have a direction, hence the use of the cross product.

Unlike “normal” multiplication and the dot product, the cross product is not commutative, i.e. it matters in which order you multiply quantities. If we find the cross product of  two forces, \mathbf{A} and \mathbf{B} then we will get a different answer to than if we had found the cross product of \mathbf{B} and \mathbf{A} , i.e. \mathbf{A} \times \mathbf{B} \ne \mathbf{B} \times \mathbf{A} . This makes sense when you consider the vector nature of the cross product: a vector to the right multiplied by a vector upwards shouldn’t produce the same result as a vector upwards multiplied by a vector to the right: the result has the same magnitude, but points in a different (opposite) direction.

Ranking Things Properly

I keep seeing things ranked improperly, so here is how to do it right.

Imagine that we have six candidates for an exam, and they score as follows. Ranking these candidates is very easy.

Name Score Rank
Abel 90% 1
Bohr 80% 2
Curie 70% 3
Dirac 60% 4
Einstein 50% 5
Feynman 40% 6

But what if two candidates have the same score? The correct way of ranking is to give both of these candidates the same rank, but then the next rank is one place lower. In the example below, Abel and Bohr both score 90% and are therefore ranked in first place; Curie then remains in third place, rather than being elevated to second.

Name Score Rank
Abel 90% 1
Bohr 90% 1
Curie 70% 3
Dirac 60% 4
Einstein 50% 5
Feynman 40% 6

This prevents a situation in which we have six participants, but the person with the lowest score is ranked fifth. If more than two participants have the same score, or if this situation occurs more than once, the same rule is applied.

Name Score Rank
Abel 90% 1
Bohr 90% 1
Curie 90% 1
Dirac 60% 4
Einstein 60% 4
Feynman 40% 6

Integer Sequences

,

Number can be broken up into many groups. Some of these groups have specific uses (for example, prime numbers are very important in cryptography) and some are just interesting for existing in the first place.

The natural numbers are what you might call “counting numbers”: 1, 2, 3, 4, … . Whether or not zero is included in the natural numbers is a matter of some discussion, and there doesn’t seem to be a consensus either way. The natural numbers does not include the negative integers, as it is not possible to have “minus one apples” or “minus two cars”.

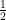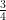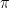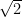The rational numbers are those that can be expressed as a simple fraction: \frac{p}{q}. Because $latex q$ can equal one, the rational numbers necessarily include the natural numbers, but also every possible other fraction: \frac{1}{2}, \frac{3}{4}, \frac{27}{31} and so on. The irrational numbers are those that cannot be expressed as fractions: e, \pi, \sqrt{2}, … and repeat indefinitely after their decimal points.

The square numbers are those that are the square of an integer: 1, 4, 9, 16, … . The cube numbers are those that are the cube of an integer: 1, 8, 27, 64 … . This process continues with x^4, x^5, and so on.

The prime numbers are those that are divisible only by one and themselves: 2, 3, 5, 7, … . The Mersenne primes are those prime numbers that are expressible as 2^n - 1, one less than a power of two: 3, 7, 31, 127, … . Sphenic numbers are the product of three primes: 30, 42, 66, 70, … . The semiprimes are natural numbers that can be expressed as the product of two prime numbers: 4, 6, 9, 10, … . There are also almost primes which are then the product of three primes, four primes, and so on. The composite numbers are those numbers that have a divisor other than one and itself, thus they are the set of numbers that are not prime.

Perfect numbers are numbers that are the sum of their divisors: 6, 28, 496, 8128, … . 6 is  a perfect number because the factors of 6 are 1, 2 and 3, and the sum of 1, 2 and 3 is 6, and so on. A number is semiperfect if it is equal to the sum of some of its divisors: 6, 12, 18, 20, … , whereas an untouchable number is a number that cannot be expressed as the sum of the divisors of any number: 2, 5, 52, 88, … . That is, there is no number whose divisors sum to 2, or to 5, or to 52, etc.

Abundant numbers are numbers whose divisors sum to a total greater than itself: 12, 18, 20, 24, … . For example, 12 is abundant because the divisors of 12 are 1, 2, 3, 4 and 6 which sum to 16 (i.e. the abundance of 12 is 4 and its abundancy is 12/4 or 3). Friendly numbers are pairs of numbers with the same abundancy: for example the abundancy of both 30 and 140 is 12/5 and therefore 30 and 140 form a friendly pair. Amicable numbers are pairs of numbers where the sum of the divisors of one number is equal to the other and vice versa. For example, 220 and 284 are amicable because the divisors of 220 add up to 284 and the divisors of 284 add up to 220. This concept can be expanded to the sociable numbers where each is part of a “loop” that arrives back at the first number (i.e. amicable numbers are sociable numbers with a period of two).  At the moment there are many known sequences of four amicable numbers, but far fewer with periods longer than this.

Weird numbers are those that are abundant but not semiperfect: 70, 836, 4030, 5830, … . The sum of their divisors is greater than the number itself, but no subset of their divisors add up to the number itself.

There are many, many other groups of numbers. Wikipedia is a good place to start looking for them.