Monthly Archives: July 2015

The World’s Longest Golf Shot

,

concorde

There is a story amongst Concorde pilots about a passenger (or in some versions it’s a pilot or the Flight Engineer) who, when the aeroplane had reached its maximum speed, hit a golf ball from one end of the cabin to the other, performing the longest golf shot in history.

Concorde’s maximum speed was Mach 2.04 or 694 metres per second, and the length of the cabin (from the door of the flight deck to the rear bulkhead) was 39.32 metres. If the golf shot was played at an average speed of 6.5 m/s it would take just over six seconds to travel the length of the fuselage.

The total distance travelled would therefore be 694 m/s multiplied by 6.5 seconds, for a total length travelled of 4200 metres. Adding on the length of the fuselage, and this gives a shot length of 4240 metres, which is 2.6 miles, so I don’t think there’s any doubt that this, if it happened, was certainly the world’s longest golf shot.

Soundex

Soundex is a system for indexing names by sound. It was designed so that homophones, words that sound the same but which are spelt differently, resolve to the same encoding. For example, the names Reid and Reed would both be encoded as R300, McDonald and Macdonald are both M235, etc.

To create a Soundex:

  1. The first letter of the Soundex is the first letter of the name.
  2. Then remove all vowels, and all occurrences of y, h and w.
  3. The remaining letters are encoded one-by-one according to their place of articulation, i.e. where in the mouth or throat the sound is formed.
    1. The labial consonants b, f, p and v, which are formed by the lips, are coded as a one.
    2. The guttural and sibilant consonants, c, g, j, k, q, s, x and z, which are formed at the back of the throat and with the tongue close to the roof of the mouth respectively, are coded as a two.
    3. The dental consonants, d and t, which are formed by the tongue against the teeth are coded as a three.
    4. The long liquid consonant l is encoded as a four.
    5. The nasal consonants, m and n, in which air escapes through the nose, are encoded as a five.
    6. The short liquid consonant r is encoded as a six.
  4. If two letters that are encoded as the same number are next to each other (e.g. the d and t in Schmidt) then the encoding is used only once.
    1. If two letters that are encoded as the same number are separated by a y, h or w then the encoding is used only once.
    2. If two letters that are encoded as the same number are separated by a vowel then the encoding is used twice.
  5. The letters are encoded one-by-one until three numbers are produced. If the name is too short, the remainder of the Soundex is encoded using zeroes.

If we use the example of Macdonald from above:

  1. First letter is M.
  2. Removing the vowels leaves us with Mcdnld.
  3. c is encoded as two, giving us M2.
  4. d is encoded as three, giving us M23.
  5. n is encoded as five, giving us M235.

Dot Product and Cross Product

There is more than one way to multiply two numbers together.

Normal everyday multiplication (e.g. 3 \times 4 = 12) isn’t always good enough for physics. If we want to multiply two vectors (quantities that have both size and direction) like force or velocity, then the direction of those vectors matters. The result of a 3 N force multiplied by a 4 N force will depend on their relative directions: if they are pointing in the same direction we will get a different answer to if they are at right angles to each other.

When multiplying two vectors, physicists use one of two products: the dot product or the cross product. Both the moment of a force (the torque) and the work done by a force are calculated by finding the product of a force and a distance, but calculating work done uses the dot product and calculating the moment of a force uses the cross product.

The dot product yields a scalar answer, an answer that does not have a direction. Work done is a scalar quantity, and doesn’t have a direction, hence the use of the dot product. The cross product yields a vector answer, which does have a direction (if you’ve ever used Fleming’s Left Hand rule to find the force acting on a current-carrying wire in a magnetic field you’ve found the cross product of those two vectors). The moment of a force does have a direction, hence the use of the cross product.

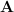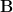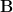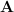Unlike “normal” multiplication and the dot product, the cross product is not commutative, i.e. it matters in which order you multiply quantities. If we find the cross product of  two forces, \mathbf{A} and \mathbf{B} then we will get a different answer to than if we had found the cross product of \mathbf{B} and \mathbf{A} , i.e. \mathbf{A} \times \mathbf{B} \ne \mathbf{B} \times \mathbf{A} . This makes sense when you consider the vector nature of the cross product: a vector to the right multiplied by a vector upwards shouldn’t produce the same result as a vector upwards multiplied by a vector to the right: the result has the same magnitude, but points in a different (opposite) direction.

Why Some Particles Don’t Decay

pair-production

Most particles do not “live” forever. The neutron, a neutral particle which resides in the nucleus of every element except hydrogen, has an average lifetime of 882 seconds (just under quarter of an hour) when outside of the nucleus. The proton has a very long lifetime and has never been observed to decay, but as Murray Gell-Mann said “Everything not forbidden is compulsory”. We therefore know that because the proton can decay, it must (eventually) decay. (Current thinking is that the lower bound, the shortest possible half-life for the proton, is at least six billion trillion trillion years, much much longer than the age of the Universe.)

But some particles: the electron, the electron neutrino, and the photon do live forever. Why is this?

When a particle decays there are a number of quantities that must be conserved, i.e. they must be the same before and after the decay. Mass-energy is conserved, so the amount of mass and energy before and after the decay must be the same. Charge is conserved, so the total charge before and after the decay must be the same.

If we take the electron as an example, it is the lightest of the charged particles, with a mass of about one eighteen hundredth of the mass of a proton. When a particle decays it must decay into a lighter particle (otherwise where would the extra mass come from?) and it must obey the conservation rules explained above. But here we have a problem: there are particles lighter than the electron (e.g. the electron neutrino) and there are particles with the same charge as the electron (e.g. the muon), but there are no particles that are both lighter than the electron and which are charged. Because the decay of an electron would violate conservation laws it is forbidden, there is nothing it could decay into, and therefore decay does not occur.