When you are diving underwater, the pressure of the gases in your lungs must be the same as the ambient pressure under water: if it were lower your lungs would implode, and if it were higher they would explode. As you go deeper and deeper, this increased pressure in your lungs forces nitrogen to dissolve into your bloodstream and from there into your tissues.
If you surface too quickly, this nitrogen is released from the tissues in the form of bubbles, and these large bubbles cause a variety of symptoms, most commonly pain in large joints (e.g. shoulders, hips an knees) and itching in the skin. (Bending these joints lessens the pain, giving the condition its colloquial name: “the bends”.) This decompression sickness can be avoided by surfacing slowly (as calculated by decompression tables or dive computers), which allows the nitrogen to leave blood and tissues in a controlled manner.
In order to lessen the risk of the bends, divers can use a different mix of gases, known as nitrox, in their scuba equipment. Nitrox contains less nitrogen (and therefore more oxygen), and this reduces the amount of nitrogen available to dissolve into the blood.
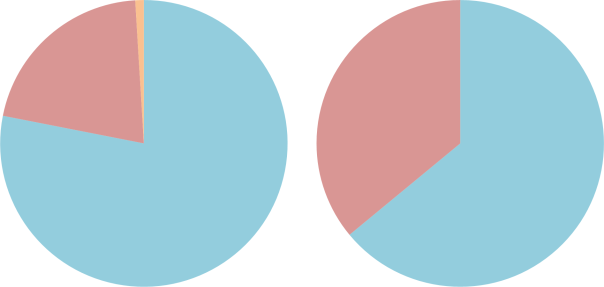
The difference between air (L) and nitrox (R). Nitrogen is coloured blue, oxygen is coloured red and other gases (carbon dioxide, etc.) are coloured orange.
For diving below about thirty metres nitrox is not suitable, for reasons best explained by the ideal gas law:
At a depth of fifty metres the pressure is about five times what it is at the surface, and your lungs would therefore contain five times as many nitrogen and oxygen (and carbon dioxide, argon, etc.) molecules as they normally would. This can lead to nitrogen narcosis, an impairment of cognitive function thought to be caused by disruption of nerve impulses. At this depth it’s not enough to simply replace the nitrogen with more oxygen, as in the case of nitrox; the extra oxygen in the lungs will lead to oxygen toxicity, a condition characterised by altered vision, drowsiness and disorientation.
To dive at this depth both the nitrogen and oxygen must be replaced by an inert gas that does not have narcotic effects. In most cases this is helium, producing a gas mix known as trimix. Different trimix “recipes” are used depending on dive depth: a high-oxygen variety for shallow depths (30-60 metres) and a lower-oxygen variety for deeper dives (below sixty metres).
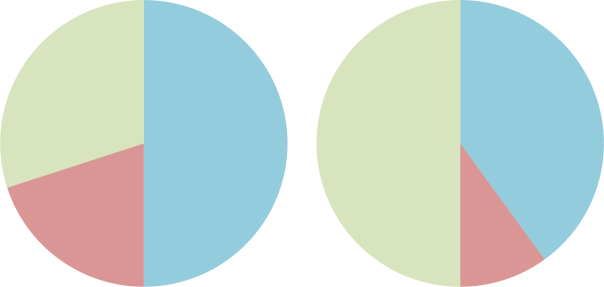
Shallow-dive (L) and deep-dive (R) trimix recipes. Nitrogen is shown in blue, oxygen in red and helium in green.
Other breathing gases are also used. During very deep dives (below 150 metres) high-pressure nervous syndrome (also known as helium tremors) is a serious risk, and thus helium is either partially or entirely eliminated, to form hydreliox or hydrox respectively. These gases are highly dangerous, as they contain both hydrogen and oxygen, which forms an explosive mixture.
