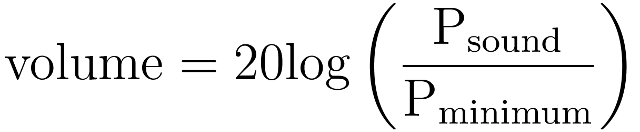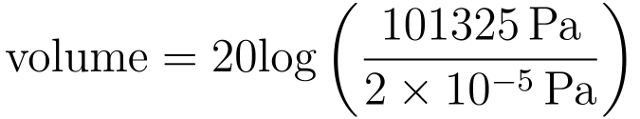Tag Archives: sound

dBA and Grey Noise

,

The human ear doesn’t hear equally well at all frequencies. The ear is much less sensitive to low frequencies, below about 1000 Hz, and to high frequencies above about 6000 Hz, and peaks in sensitivity at around 2500 Hz.

A microphone doesn’t have the same issue. This means that after sound is recorded, a filter is applied so that the recorded sound mimics what a human ear would have heard. This filter is called A-weighting, and the volume of sound that is recorded is referred to as dB(A).

dBA-weighting-linear
dB(A) weighting (linear frequency scale)

dBA-weighting-logarithmic
dB(A) weighting (logarithmic frequency scale)

White noise is often taken to be equally loud at all frequencies, but this is not the case: although the sound that is produced is equally loud at all frequencies, this is not what the ear hears. Grey noise is white noise that has been A-weighted so that it is heard to be equally loud at all frequencies.

White noise:

Grey noise:

Adverts are not louder than TV shows

It is a common complaint that the adverts played during TV shows are louder than the TV shows themselves. This, however, is not the case: without adjusting the volume of your TV this would be impossible.

What is different between adverts and TV shows is the difference between the loud and the quiet parts. The loudest parts are the same volume, but the quietest parts of the adverts are louder than the quietest parts of the TV shows, and this gives the adverts the impression of being louder overall.

As an example, I took the first twenty seconds of Kalimba by Mr Scruff (one of the sample songs included with Windows 7) and compressed it.

Original version:

Compressed version:

The compressed version appears louder overall, but a comparison of their waveforms in Audacity shows that the loudest parts of both have the same volume.

waveform-comparison

The original waveform is shown at the top and the compressed waveform is shown at the bottom.
The scale on the y-axis is the same for both.

The USA has enacted a law, the Commercial Advertisement Loudness Mitigation Act (CALM Act), which mandates that the average volume of adverts may not exceed the volume of the TV shows during which they play, which does away with this compression trickery.

Datalogging the lesson

, ,

My department recently bought some nifty portable dataloggers. I decided to test one out during my last two periods with 5PHC by measuring the volume of sound in the room during the lesson’s ninety minute duration.

Because the volume of sound spans many orders of magnitude it’s not really possible to measure all possible volumes accurately. I used two different sensors: one measuring from 30dB to 70dB and one measuring from 50dB to 90dB. When a measurement was picked up by both devices I used the average value.

The original data is very noisy, partially because the sampling was done five times per second and partially because the volume of sound produced by twenty-one fifteen and sixteen year-olds can vary very quickly.

I averaged the data over a moving thirty second period to produce a more useful graph:

The average volume during the whole lesson was 56.9dBA. The “A” in “dBA” indicates that the sound pressure level sensor I used was using A-weighting that attempts to reproduce the human ear’s response to sound.

You can see gradual increases in volume punctuated by shouts of “QUIET!” that cause the volume to drop very suddenly.

The loudest sound

Sound is created by vibrating objects. As an object, such as a loudspeaker’s diaphragm moves back and forth it compresses the air, causing changes in pressure. These changes in pressure cause your eardrum to move back and forth and these back-and-forth movements are translated by your brain into sound. Larger, louder, movements cause greater changes in pressure.

A tuning fork creates compressions (higher pressures) and rarefactions (lower pressures) in the air.

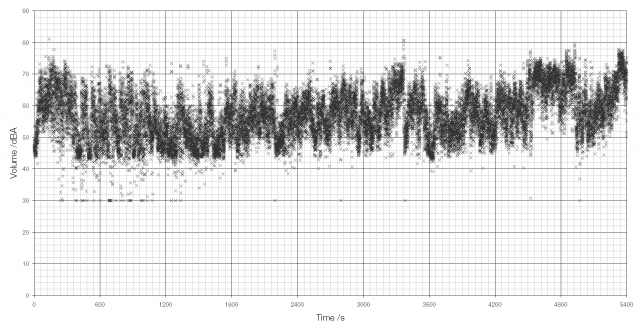
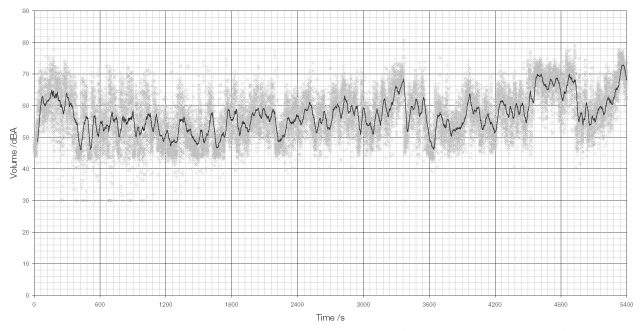
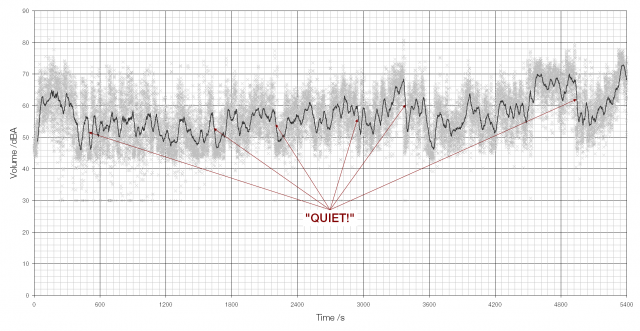
The human ear is incredibly good at detecting changes in air pressure; it can detect the greatest range of stimuli of all your senses. The quietest sound that the ear can hear is the smallest change in pressure that it can detect: 20 µPa, less than a billionth of atmospheric pressure. To calculate the volume of a sound you must compare the pressure change caused by the sound with this smallest detectable change.

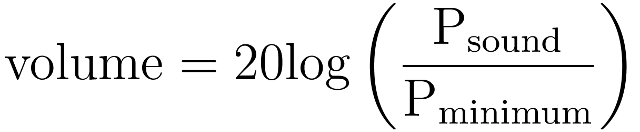
The decibel* scale is logarithmic. One bel represents a tenfold increase in pressure so a 50 dB sound is ten times louder than a 40 dB sound. The average volume of human speech is about 60 dB and the threshold of ear pain is 130 dB, some 107 or ten million times louder.

Because a sound wave consists of alternating low and high pressures there comes a point at which the sound is so loud that the rarefaction (low) pressure is the lowest possible pressure: a vacuum at 0 Pa. This corresponds to a compression pressure of one atmosphere or 101325 Pa. If we put these figures into the equation for volume we find:

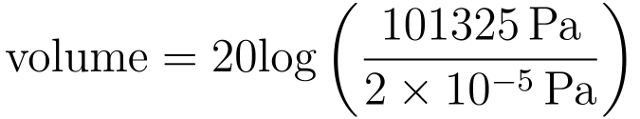
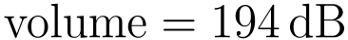
So there you have it: the loudest possible sound is 194 dB. It has often been said that the loudest ever recorded sound was the eruption of Krakatoa in 1883 which was heard from nearly 5000 km away. The pressure wave created by the eruption was measured to be at least 20000 Pa, equi­valent to a volume of 180 dB, 101.4 or twenty-five times quieter than the loudest possible sound.

* The prefix deci- indicates a tenth.