Monthly Archives: October 2012

Surviving acceleration

,

How fast can you accelerate, or decelerate, and live to tell the tale?

In this context, acceleration and deceleration are usually measured in ‘G’s, multiples of the acceleration due to gravity. For example, if you crashed a car travelling at 70 miles per hour into a wall, and it took you one second to come to a stop this would be a deceleration of 35.8 metres per second per second, which is equivalent to an deceleration of 3.65 G. If the person in the car had a weight of 1000 newtons (≈100 kg) they would feel a force pushing them forwards against their seatbelt of 3650 N.

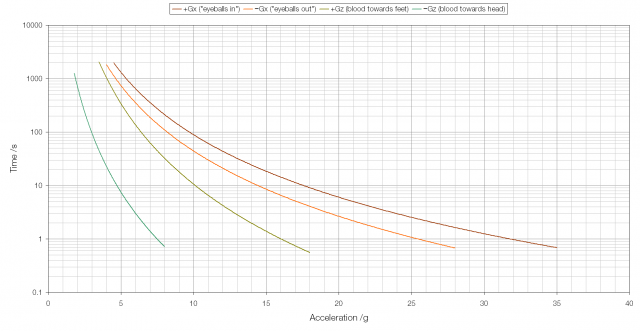
G-forces on the human body are described in two ways*: Gx which is along an axis running horizontally through the chest at a right angle and Gz which is along an axis running vertically downwards through the head and feet. A positive Gx is described as “eyeballs in” and a negative Gx as “eyeballs out”; a positive Gz pushes blood towards the feet and a negative Gz pushes blood towards the head.

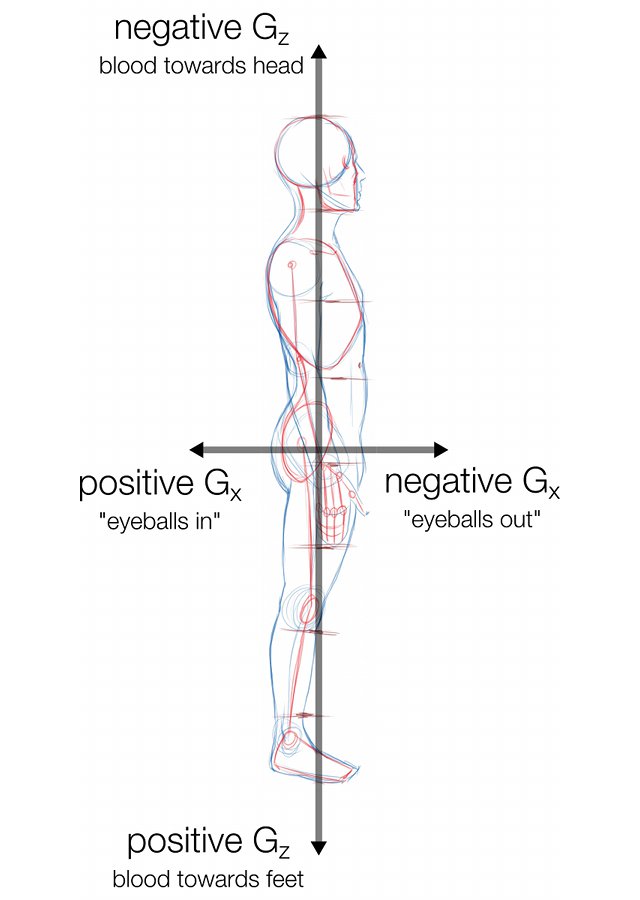
The human body responds differently to acceleration in different directions.

For example: a human being can survive an “eyeballs in” 5G acceleration for about 1500 seconds, but an “eyeballs out” 5G acceleration for only half of that. Moving vertically, with blood towards the feet, a 5G acceleration can only last for 350 seconds before death occurs; but with blood towards the head for only about 8 seconds.

It seems that the human body is least sensitive to “eyeballs in” and “eyeballs out” accelerations, which makes sense when considering that human beings are far more prone to experience these accelerations than others. It’s easier to survive blood rushing to the feet than it is to survive blood rushing to the head, as increased blood pressure in the head can cause blood vessels in the brain to burst.

* It seems that very little work has been done on how the body responds to sideways accelerations.

How are mushroom clouds formed?

, ,

Mushroom clouds (perhaps more properly known as pyrocumulus clouds) are traditionally associated with nuclear explosions, but any sufficiently large explosion (for example, a volcanic eruption) will create a mushroom cloud.

The mushroom cloud resulting from the Priscilla test of Operation Plumbbob.

When a large explosion occurs a cloud of very hot gas is created. This hot gas, being less dense than the surrounding air, rises rapidly upwards. As this cloud of hot gas rises it pushes against the air above it and this air resistance causes the top layer to move sideways whilst the hotter gas below continues rising upwards, creating a swirling doughnut-shaped vortex (in the photograph above a very hot “filament” is visible at the centre of this vortex). As the “cap” rises this swirling vortex pulls in cooler air from ground level, creating the “stalk” on which the cap sits.

The formation of a mushroom cloud during the Tumbler-Snapper series of nuclear tests.

The shape of a mushroom cloud is the result of a Rayleigh-Taylor instability at the interface between the hot less-dense and cold more-dense air. These instabilities occur in a number of different situations, and can be easily demonstrated at home by dropping coloured oil into water, creating tiny upside-down mushroom clouds as shown below in photographs by James Riordon of AIP.

The simulated formation of a Rayleigh-Taylor instability.

Tog

, ,

Duvets are often rated by their “tog” rating. But what is tog?

Tog is a measure of a duvet’s thermal resistance. It measures the extent to which the duvet resists the transfer of thermal energy through it. One tog is equal to one-tenth of a metre squared kelvin per watt or 0.1 m²K/W. Thermal resistance can be a bit difficult to understand, but the reciprocal of thermal resistance, the thermal conductance, is a bit easier to grasp.

A one tog duvet would have a thermal resistance of 0.1 m²K/W and a thermal conductance of 10 W/m²K, a two tog duvet would have a thermal resistance of 0.2 m²K/W and a thermal conductance of 5 W/m²K, and so on.

A lightweight summer duvet* has a tog rating of about four, so its thermal conductance is 2.5 W/m²K. This means that 2.5 watts of thermal energy will move through each square metre of the duvet for every one kelvin difference in temperature between the sides of the duvet.

Whilst sleeping the average person puts out about seventy watts of heat. Some of this heat will be radiated into the mattress, and some will leak out around the head and neck and edges of the duvet, but it’s not unreasonable to think that around fifty watts is going into the air surrounding the body underneath the duvet.

To maintain a constant temperature underneath the duvet the amount of heat lost must be equal to the amount of heat output by the body. If an eight tog (1.25 W/m²K) autumn duvet has an area of three square metres then this break-even point will be reached when the difference in temperature between the two sides is about thirteen degrees (50 ÷ (3 × 1.25)). Given a skin temperature of 35°C this duvet will therefore keep you at a constant temperature in a room at a temperature of 22°C. If the room is colder than 22°C then the air underneath the duvet will gradually cool down and the body will increase its rate of heat production to compensate. If the room is hotter than 22°C then the air around the body will continue to increase in temperature (until it reaches the same temperature as the body) making you uncomfortably hot and will probably cause you to throw off the duvet or stick your leg out from underneath the covers to increase the rate of heat loss.

If the duvet in the example above is replaced with a four tog summer duvet with a conductance of 2.5 W/m²K then the room would have to be a scorching 29°C, but it’s unlikely that in this situation you would want a constant temperature – you’d want to remain cool overnight. If it was replaced with a twelve tog winter duvet (conductance = 0.83 W/m²K) then the room could go down to 15°C before a net heat loss occurred.

All the calculations above are based on some unreasonable assumptions, the most obvious one being that heat is not lost throughout the whole three square metre surface of the duvet. If a person is “using” only half this area then the numbers involved change to reflect more realistic values: for a winter duvet the temperature difference required can be greater and for a summer duvet it can be smaller. The calculations also ignore the effect of any heat radiated into the mattress below the person and the insulating effect that this mattress would have.

* John Lewis classifies summer duvets as those rated at between three and four-and-a-half tog, spring/autumn duvets as those between seven and ten-and-a-half tog and winter duvets as those between twelve and thirteen-and-a-half tog.

The Trivers-Willard hypothesis

,

The Trivers-Willard hypothesis states that when conditions are good, parents have more male offspring; and when conditions are poor, parents have more female offspring. The thinking behind this is that in favourable conditions males will be able to mate with many females before they die and have a greater chance of passing on their genes; and when conditions are poor males will not be able to mate with as many females and are more likely to be out-competed, and therefore a female will have more chance of passing on genetic material than any particular male.

The Trivers-Willard hypothesis seems to hold true for human beings. In a study of the Forbes Billionaires List it was found* that the children of billionaires were 60% male, and if only male billionaires were considered then this percentage rose to 65%. The effect was the same whether the billionaires were self-made or had inherited their fortunes, suggesting that if there was a biological reason for success in business it was not relevant in selecting the sex of offspring.

It is uncertain what causes the Trivers-Willard effect, but a 2001 paper suggested† that “condition” was linked to the availability of food and of glucose in this food, and that the presence of elevated levels of glucose in the mother’s blood favours the survival of male blastocysts. This has led to the idea of the “Trivers-Willard Diet“, designed to enable parents to select the sex of their offspring.

* Elissa Cameron and Fredrik Dalerum, “A Trivers-Willard Effect in Contemporary Humans: Male-Biased Sex Ratios among Billionaires”, PLoS ONE 4(1) (2009): e4195. DOI: 10.1371/journal.pone.0004195.

† Melissa Larson et al, “Sexual dimorphism among bovine embryos in their ability to make the transition to expanded blastocyst and in the expression of the signaling molecule IFN-τ”, Proc Natl Acad Sci 98(17) (2001): 9677-9682. DOI: 10.1073/pnas.171305398.

Nuclear art forgery

, ,

Nuclear weapons* are triggered by neutron initiators, devices that produce a sudden burst of neutrons on activation. They are most often constructed from a mixture of beryllium-9 and polonium-210. The polonium emits high-energy alpha particles, and when brought into contact with the beryllium it causes the beryllium to transmute into carbon with the release of a neutron. This neutrons causes an atom of uranium-235 to split (to fission) and in the process release a huge amount of energy and more neutrons that go on to cause further fissions.

This uncontrolled chain reaction results in the production of many exotic isotopes, as the uranium atoms split to form “chunks” of other elements. For example, it was in the aftermath of the ‘Ivy Mike’ test of the first thermonuclear bomb that the elements einsteinium and fermium were discovered.

The existence of rare isotopes can be used to demonstrate that a painting or other work of art was not produced before the 1940s or 1950s, when nuclear weapons testing was at its peak. Strontium-90 and caesium-137 are isotopes that did not exist in nature before the age of nuclear weapons and which permeate soils and are taken up by plants and other living things as they are very soluble in water. If these organic materials are used in the production of paints, or binders for paint, or in other ways in a piece of art then the presence of Sr-90 or Cs-137 can be used to prove that the item in question was created after the beginning of the nuclear age.

* This paragraph details the operation of a fission bomb. Fusion (thermonuclear) bombs work differently, but all use a fission stage to initiate the fusion process.