Many people assume that the terms “centre of mass” and “centre of gravity” are synonymous, but this is not the case.
Centre of mass is the point at which the distribution of mass is equal in all directions, and does not depend on gravitational field. Centre of gravity is the point at which the distribution of weight is equal in all directions, and does depend on gravitational field.

A toy bird balances when a pivot is placed at its centre of gravity.
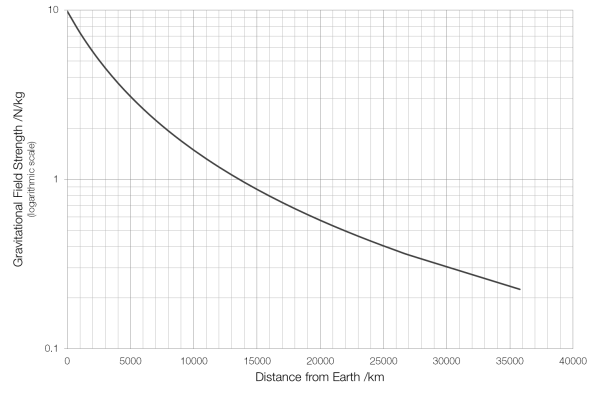
The centre of mass and the centre of gravity of an object are in the same position if the gravitational field in which the object exists is uniform. In most cases this is true to a very good approximation: even at the top of Mount Everest (8848 metres) the gravitational field strength is still 99.6% of its standard value. You are unlikely ever to experience a difference between centre of mass and centre of gravity, as the gravitational field in which you find yourself is extremely uniform.
But if the gravitational field strength were greater towards your feet and weaker towards your head, then your centre of gravity would be below your centre of mass, perhaps somewhere around your knees. If the gravitational field strength were greater towards your head, and weaker towards your feet, then your centre of gravity would be above your centre of mass, perhaps somewhere around your shoulders.
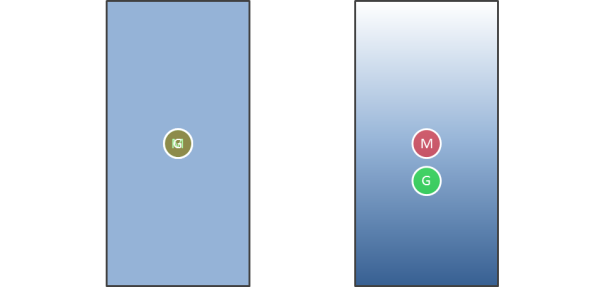
The object on the left, in a uniform gravitational field, has overlapping centres of gravity and mass. For the object on the right, in which the gravitational field is stronger towards its base, the centre of gravity is below the centre of mass. Approaching a black hole the gradient of the gravitational field would be infinitely “steep”, leading to an incredible difference in gravitational field and death by spaghettification for anyone falling into a black hole.
 An apple floats in mid-air aboard the ISS.
An apple floats in mid-air aboard the ISS.