Tag Archives: gravity

You can see more than half of a neutron star

,

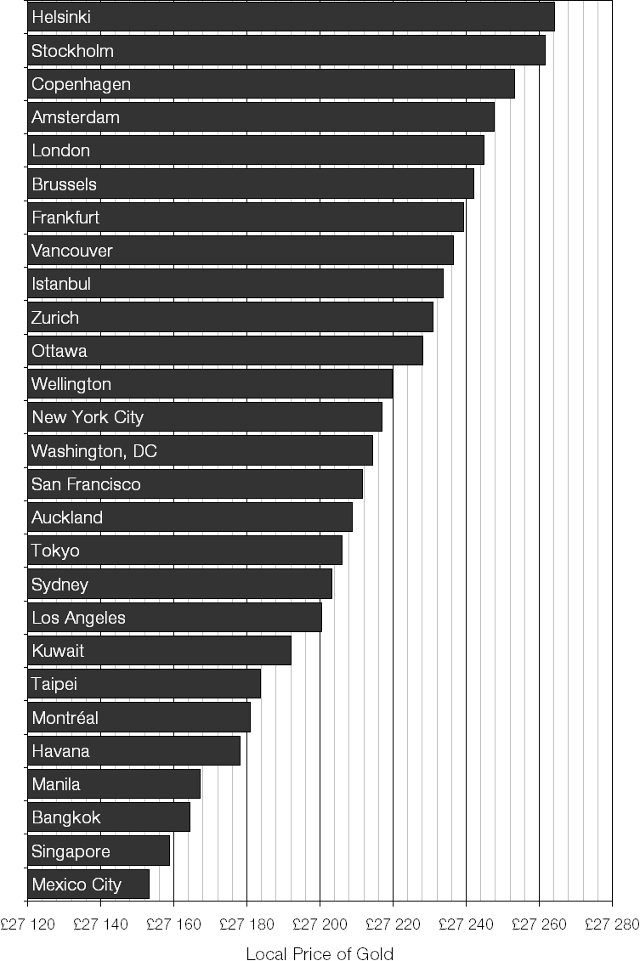
Common sense dictates that if you look at a spherical object like a ball or a planet you can only see half the surface area of that object. But this is not true for neutron stars.

A neutron star is formed when the core of a relatively large star collapses in on itself in a supernova. Neutron stars are incredibly dense: one teaspoon of neutron star can have a mass of more than five trillion kilograms.

One of the best elaborations of Einstein’s Theory of General Relativity was given by John Wheeler:

“Mass tells space-time how to curve, and space-time tells mass how to move.”

But if space-time is curved then anything passing through space, whether it is matter or light, will follow a curved path. The gravitational field of a neutron star is so strong that it warps space, and warps space to such an extent that light emitted behind the star is warped around.

Diagram of a neutron star, viewed face-on.

In the diagram above each chequered section is 30° × 30°; note that both poles of the neutron star are clearly visible. The highlighted section on the right-hand diagram shows the area that would normally be visible if gravitational distortion were not present.

Normally 180° of latitude and longitude would be visible, but in this case the figure is nearly 260°, meaning that more than 70% of the neutron star’s surface area is visible.

Does your weight change in a lift?

, ,

The simplest answer to the question of whether your weight changes when you ride in a lift is ‘no’. Your weight, being the force with which the Earth pulls down upon you due to gravity, does not vary with speed or acceleration.

It does, however, feel like your weight changes when you ride in a lift. Because your weight is the force between you and the Earth (and between the Earth and you) you cannot actually feel your own weight; what you feel is the ground pushing up against you (the normal reaction force). Because of Newton’s Third Law (“each force has an equal but opposite reaction force”) this force is equal to your weight pushing down on the Earth.

When the lift accelerates and decelerates the force that the cables and motors exert on the lift is either added to, or subtracted from, the force with which the floor of the lift pushes up on you. This is what makes you feel heavier and lighter.

I used a PASCO force platform and a SPARK datalogger to measure the apparent change in my weight as I rode downwards in a lift.

You can see a drop in apparent weight as the lift accelerates downwards, this then returns to normal as the lift travels at constant speed before rising again as the lift decelerates. By measuring the peak forces and using Newton’s Second Law of Motion I can calculate some approximate values for the maximum acceleration and deceleration of the lift in question: for the lift at school these values were 0.569 m/s2 and −0.625 m/s2, showing the lift decelerates at a significantly higher rate than it accelerates.

Were you in a lift that was accelerating downwards at the same rate as gravity (9.81 metres per second per second) you would feel weightless; were you in a lift that was accelerating upwards at the same rate you would feel like you weighed twice as much.

Making money from gravity

,

The gravitational field strength of a planet depends on size and mass, and the Earth is not uniform in either respect. Because of its rotation Earth’s radius is 21km greater at the equator than at the poles and water (which covers 71.1% of Earth’s surface) is much less dense than the rock that covers the remaining 28.9%.

These two factors, combined with the centripetal force effect of Earth’s rotation itself mean that the strength of Earth’s gravitational field varies across its surface.

This gravity map from the GRACE satellite shows the variation of the gravitational field across Earth’s surface; red indicates higher gravitational field strength and blue lower.

The place with the lowest gravitational field strength is Mexico City (9.779 N/kg, 0.28% below average) helped by it’s elevation, more than two thousand metres above sea level. The highest gravitational field strength is found in Helsinki (9.819 N/kg, 0.13% above average) at a latitude of 60°N.

Because people confuse mass and weight and because Earth’s gravitational field changes the same bar of gold will be measured to have a different mass in different locations. One kilogram of gold will be measured to have a mass of 997.18 grams in Mexico City and 1001.3 grams in Helsinki.

This lends itself to a money-making scam: if I buy gold in Mexico City and sell it in Helsinki I can make a profit of £111 per kilogram (at the current price of £27230 per kilogram). In order to pay for my plane ticket (about £1500) I only need to carry thirteen and a half kilograms of gold (a cube with 9cm sides) with me, though this will cost me about £367000.

You can download the Excel spreadsheet I used to do the calculations for this post: gravity-gold-calculator (31kB, .xls).

Heavier going up, lighter coming down

,

If you’ve every felt a little bit heavier in a lift going up, or a little bit lighter in a lift coming down, you’re not imagining it.

Imagine standing on a set of scales in a lift. The Earth pulls you down onto the scales and the scales push back on you with an equal force – that’s the force that the scales read.

Einstein’s equivalence principle, part of the framework of general relativity, is that it is impossible to tell the difference between acceleration due to gravity and acceleration due to an external force*. If the lift is accelerating upwards this must be because a force is exerted upon the lift in an upward direction and as this is in addition to the force of the scales pushing upward, you feel heavier.

Some of the world’s fastest elevators, those found in the Taipei 101, go from stationary to 60 km/h in sixteen seconds, which means they accelerate at 1.05 m/s². When this is added to the acceleration due to gravity (9.81 m/s²) it increases the weight of an object by just under 11% – an 80 kg man would feel like he had a mass of 89 kg. When decelerating, the opposite is true – an 80 kg man would feel like he had a mass of 71 kg.

If the lift was accelerating downward quickly enough, at 9.81 m/s², then the person inside would feel completely weightless. This is how weightlessness is simulated in aircraft, accelerating downward in a powered dive at the same rate as gravity.

* Einstein’s equivalence principle is actually about the difference between inertial mass and gravitational mass but the difference isn’t particularly important here.