Monthly Archives: September 2014

Base Bleed Artillery

,

base-bleed-patentMost of the drag on an artillery shell comes from friction between the nose of the shell and the air, as the shell pushes air out of the way at very high speeds. But some of the drag on a shell comes from the sucking effect of the vacuum left behind the shell as it pushes air in front out of the way faster than air can move to fill the space left behind.

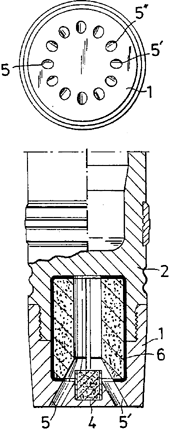
To combat this, many artillery shells employ a system called base bleed in which the shell produces gas at its rear to fill this vacuum. This gas produces very little thrust, but by reducing the effect of the vacuum it increases the range of the shell enormously, typically by around 30%. On the diagram on the right (taken from this patent) the top image shows a view from below, with the gas generator’s exhaust labelled “5”. The housing of the gas generator is labelled “1” and the casing of the shell “2”. The igniter that starts the gas generator is labelled “4” and the fuel charge that produces the gas is labelled “6”.

The Difference Between Centre of Mass and Centre of Gravity

Many people assume that the terms “centre of mass” and “centre of gravity” are synonymous, but this is not the case.

Centre of mass is the point at which the distribution of mass is equal in all directions, and does not depend on gravitational field. Centre of gravity is the point at which the distribution of weight is equal in all directions, and does depend on gravitational field.

balancing-bird-toy

A toy bird balances when a pivot is placed at its centre of gravity.

The centre of mass and the centre of gravity of an object are in the same position if the gravitational field in which the object exists is uniform. In most cases this is true to a very good approximation: even at the top of Mount Everest (8848 metres) the gravitational field strength is still 99.6% of its standard value. You are unlikely ever to experience a difference between centre of mass and centre of gravity, as the gravitational field in which you find yourself is extremely uniform.

But if the gravitational field strength were greater towards your feet and weaker towards your head, then your centre of gravity would be below your centre of mass, perhaps somewhere around your knees. If the gravitational field strength were greater towards your head, and weaker towards your feet, then your centre of gravity would be above your centre of mass, perhaps somewhere around your shoulders.

grav-com-cog

The object on the left, in a uniform gravitational field, has overlapping centres of gravity and mass. For the object on the right, in which the gravitational field is stronger towards its base, the centre of gravity is below the centre of mass. Approaching a black hole the gradient of the gravitational field would be infinitely “steep”, leading to an incredible difference in gravitational field and death by spaghettification for anyone falling into a black hole.

Rotational Kinetic Energy and Moment of Intertia

The kinetic energy of an object moving in a straight line is easy to understand:

E_\textrm{k} = \frac{1}{2}mv^2

where E_\textrm{k} is kinetic energy, m is the mass of the object and v is the object’s velocity.* If the mass of the object doubles, the kinetic energy doubles; and if the object’s velocity double the kinetic energy is quadrupled.

Kinetic energy is the energy that an object has due to the fact that it is moving, and therefore an object that is rotating must have kinetic energy. But if it’s rotating, staying in one place, then its velocity is zero and thus we can’t use the equation above.

The kinetic energy of a rotating object is given by:

E_\textrm{k} = \frac{1}{2}I\omega^2

where E_\textrm{k} is the rotational kinetic energy, \omega is the angular velocity (i.e. the angle turned through divided by the time taken, measured in degrees per second or radians per second). The complicated part of the equation is I, which is the moment of inertia.

The moment of inertia can be thought of as the rotational equivalent of mass; the degree to which an object resists a change in its (rotational) motion. The moment of inertia depends on the shape of the object and the way it rotates. For example: the moment of inertia of a rod rotating about its centre, and a rod rotating about its end, are very different.

moment-of-inertia-rods

The moment of inertia of the rod on the left, rotating around its end is I = \frac{ml^2}{3}, where m is the mass of the rod and l is its length. The moment of inertia of the rod on the right that rotates around its centre is I = \frac{ml^2}{12} and thus if the rods have the same lengths and masses, and rotate at the same rate, the kinetic energy of the rod on the left will be four times greater.