Tag Archives: kinematics

Rotational Kinetic Energy and Moment of Intertia

The kinetic energy of an object moving in a straight line is easy to understand:

E_\textrm{k} = \frac{1}{2}mv^2

where E_\textrm{k} is kinetic energy, m is the mass of the object and v is the object’s velocity.* If the mass of the object doubles, the kinetic energy doubles; and if the object’s velocity double the kinetic energy is quadrupled.

Kinetic energy is the energy that an object has due to the fact that it is moving, and therefore an object that is rotating must have kinetic energy. But if it’s rotating, staying in one place, then its velocity is zero and thus we can’t use the equation above.

The kinetic energy of a rotating object is given by:

E_\textrm{k} = \frac{1}{2}I\omega^2

where E_\textrm{k} is the rotational kinetic energy, \omega is the angular velocity (i.e. the angle turned through divided by the time taken, measured in degrees per second or radians per second). The complicated part of the equation is I, which is the moment of inertia.

The moment of inertia can be thought of as the rotational equivalent of mass; the degree to which an object resists a change in its (rotational) motion. The moment of inertia depends on the shape of the object and the way it rotates. For example: the moment of inertia of a rod rotating about its centre, and a rod rotating about its end, are very different.

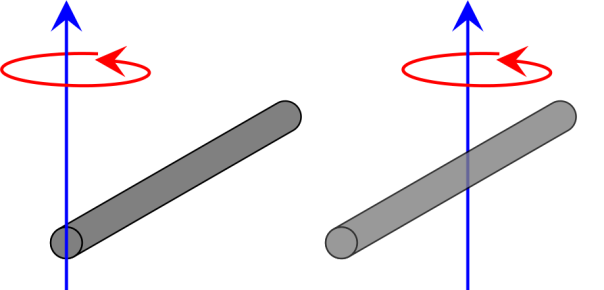
moment-of-inertia-rods

The moment of inertia of the rod on the left, rotating around its end is I = \frac{ml^2}{3}, where m is the mass of the rod and l is its length. The moment of inertia of the rod on the right that rotates around its centre is I = \frac{ml^2}{12} and thus if the rods have the same lengths and masses, and rotate at the same rate, the kinetic energy of the rod on the left will be four times greater.

Jerk, Jounce, Snap, Crackle and Pop

,



Physicists are obsessed by rates: how quantities change over time. The rate of change of the number of nuclei in a radioactive sample tells us how radioactive something is; the rate at which the chemicals in a reaction change tells us how reactive something is; and so on.

If we start by looking at the displacement of an object (i.e. the distance from where it started to where it currently is) then when we look at the first derivative (by time) of displacement, (i.e. dividing the displacement of an object for how long it took to be displaced) we have calculated the object’s velocity.

v = \frac{dx}{dt}

If we look at the rate of change of velocity, the second derivative (by time) of the object’s displacement (i.e. the rate of change of the rate of change of its displacement), then we have calculated the object’s acceleration.

a = \frac{dv}{dt} = \frac{d^2x}{dt^2}

If we now look at the rate of change of acceleration, the third derivative of the object’s displacement (i.e. the rate of change of the rate of change of the rate of change of its displacement) then we have calculated the object’s jerk.

j = \frac{da}{dt} = \frac{d^2v}{dt^2} = \frac{d^3x}{dt^3}

The first two derivatives of displacement, velocity and acceleration, are well known and reasonably well-understood by most people. But jerk is a little bit more difficult to understand. If we apply a force to an object it will accelerate, and we usually assume that this force is applied instantaneously. But this is not correct – it takes time to apply a force. As a result, the rate of acceleration will not be constant, and thus we have the jerk.

It may be easier to understand the concept of a third derivative by looking at an example from economics: inflation. US President Richard Nixon once famously said “the rate of increase of inflation is decreasing”, using a third derivative in the process.

The rate of inflation is the rate at which prices increase over time, and this is therefore the first derivative of price. The rate of the increase in inflation is a second derivative, and if this itself is decreasing then that is a third derivative. That is, in Nixon’s case, prices were increasing (i.e. inflation was positive), and this rate of inflation was itself also increasing, but the rate at which it increasing was decreasing.

The fourth derivative of an object’s displacement (the rate of change of jerk) is known as snap (also known as jounce), the fifth derivative (the rate of change of snap) is crackle, and – you’ve guessed it – the sixth derivative of displacement is pop. As far as I can tell, none of these are commonly used.