Tag Archives: map

Earth Sandwich

,

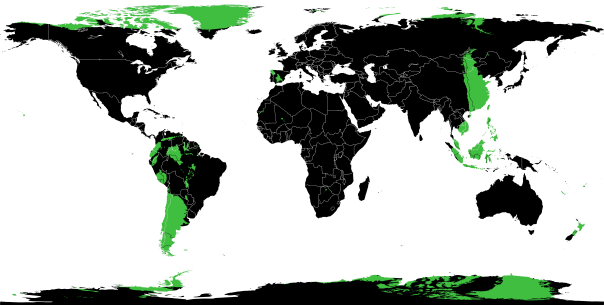
What is the significance of the areas highlighted in green on the map below?

earth-sandwich-results

Click for a much larger version.

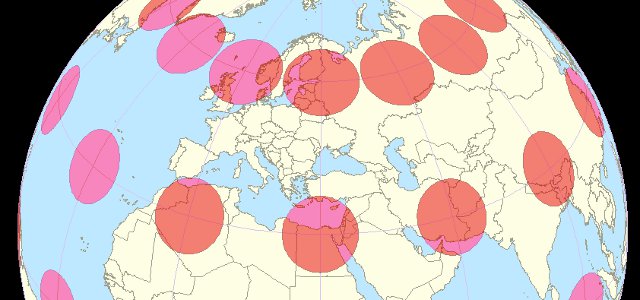
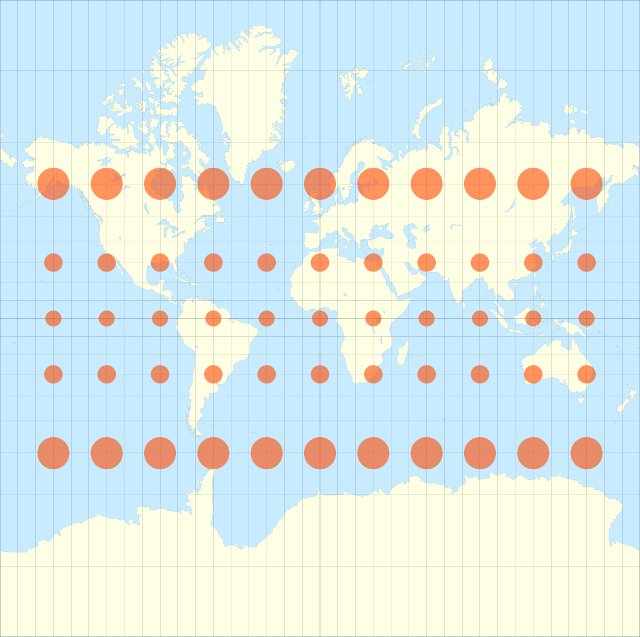
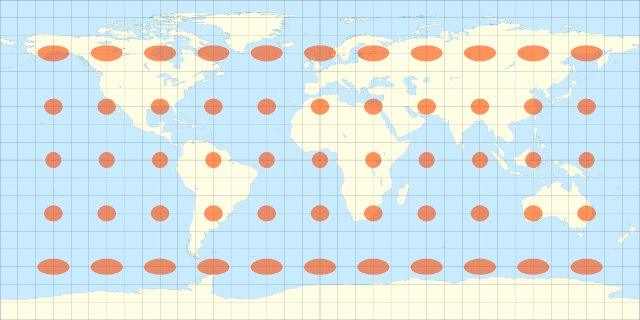
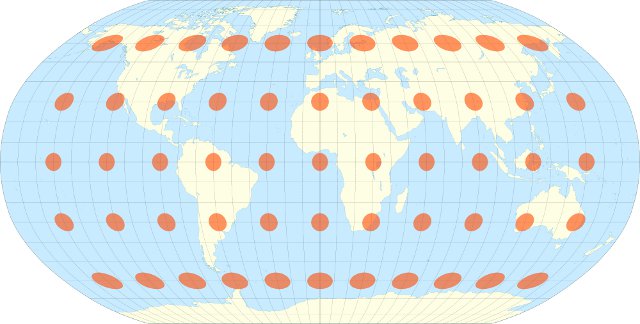
The highlights indicate areas where there is land on both sides of the globe – that is, areas where you could create a successful Earth Sandwich.

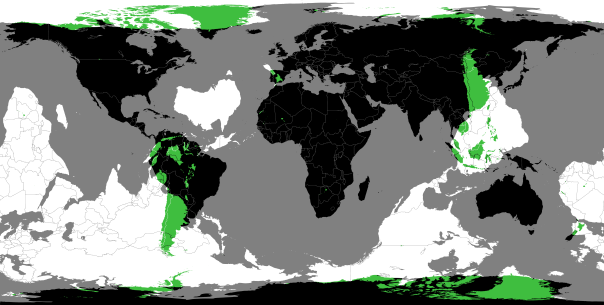
For example, if you started in Northern Argentina and drilled through the Earth’s core you would end up in Southern China. If instead you started in southern Argentina you’d end up either in Mongolia or Russia. It’s a little bit easier to understand if you look at the overlaid maps below.

earth-sandwich-overlay

There are significant areas of overlap between South America and around the South China Sea, and between Northern Canada & Greenland and the Antarctic.

There are also some interesting smaller spots, for example where Spain/Portugal (and a tiny portion of Morocco) and New Zealand overlap, or the Islands of Hawai’i and Botswana.

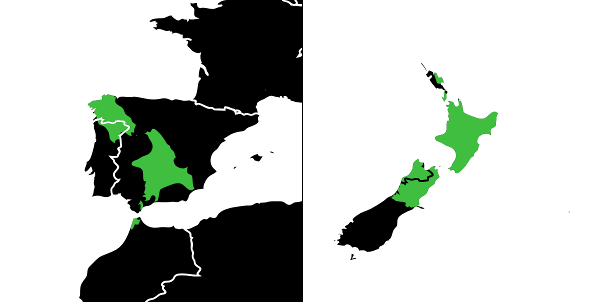
spain-nz

Spain/Portugal/Morocco and New Zealand

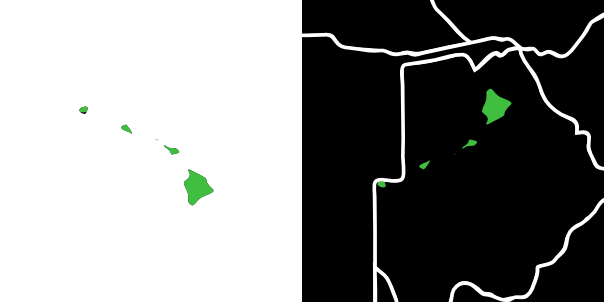
hawaii-botswana

Hawai’i and Botswana

Poverty and the wind

, ,

A map of poverty* in London clearly shows a clustering of poorer areas to the north-east of the city.

There is a very simple reason for this, and it’s the same reason that poorer areas are found towards the north and east of most large and old towns in the UK: the prevailing wind.

Because of its position to the north-east of the Atlantic Ocean, the prevailing wind in the UK is from the south-west (i.e. blowing north-east). Any atmospheric pollution produced in London – and in the 1800s and 1900s that was be a lot of pollution – would be blown to the north-east, making that area less attractive and therefore cheaper to live in.

You can explore poverty in the UK using the interactive Google Map below, which I found via a story in The Grauniad:

* The data used is the 2007 Index of Multiple Deprivation, and the mapping is by London Profiler.

Yearly variations in the storage of CO2 by plants

,

The maps below show the production of carbon dioxide by plants versus its absorption. The greenest areas are those that are storing the most carbon, where plant growth is greatest (grey areas indicate no plant life).

The map above shows the world in August, summer in the northern hemisphere. Note the particularly heavy absorption of carbon dioxide in the tropical rainforests of Bolivia, Peru, Brazil and other South American countries and the production of algae off the west coast of Africa.

The map below shows a much different picture, the world in December when it is winter in the northern hemisphere and summer in the southern hemisphere.

Storage of carbon dioxide by plants reaches its lowest point in December, causing the atmospheric concentration of carbon dioxide to peak.

It’s easy to see why plant production peaks when maps of incoming solar radiation for August and December are compared. The bright yellow areas are those receiving high amounts of incoming sunlight; the dark red areas receive the least.

August 2010

December 2010

Also interesting to compare are maps showing the balance of radiation. The orange areas in the maps below are those which are absorbing more radiation than they emit, and green areas are those which emit more radiation than they absorb.

The difference between areas near the equator that receive year-round sunlight and areas nearer the poles where sunlight is seasonal is quite marked; Greenland remains a net radiator throughout the year due to northerly position and its year-round white reflective coating of ice and snow.

August 2010

December 2010

Tissot’s indicatrix

,

Flat two-dimensional maps are unable to accurately represent the curved three-dimensional surface of the Earth; some distortion of area, shape, distance and/or scale is unavoidable. Tissot’s indicatrix, invented by French mathematician and cartographer Nicolas Tissot, is a method for assessing and indicating the amount of distortion present in a map.

The indicatrix is created by placing an array of tiny circles on the Earth’s surface and then mapping those circles along with the rest of the Earth’s features; the size of the circles is then increased to make them visible.

The Mercator projection maintains correct shapes but exaggerates the size of land masses as distance from the equator increases. On the Mercator projection Greenland appears to have a similar area as Africa, despite being only 7% of the size in reality; it also makes Antartica look much larger than it is.*

The equirectangular projection preserves approximate size at the expense of shape: land masses away from the equator are distorted both horizontally and vertically but distances along meridians (lines of longitude) are preserved.

The use of rectangular projections for whole world maps is now widely discouraged; they are considered suitable only for small areas where any distortion will be negligible.

The non-rectangular Robinson and Winkel tripel projections both attempt to find an acceptable compromise between distortions of shape and distance.

Robinson projection

Winkel III projection

* The Mercator projection’s early popularity was due to its heavy use by sailors – on a Mercator map a constant heading yields a straight line.

Geodesics

, ,

What’s the shortest way to travel from London Heathrow airport (LHR) to JFK International airport (JFK)?

You’d think it would be a straight line like this:

But you’d be wrong. The shortest distance between LHR and JFK is actually a curve:

This is because the “shortest distance between two points is a straight line” rule only applies to a flat surface: normally when you use a map it covers such a small area that the curvature of the Earth isn’t noticeable, but on a map of the world it becomes important.

Because a map takes the curved spherical surface of the Earth and maps it onto a flat surface no map can accurately show the whole world – every possible map projection is cursed to distort the size and/or shape of countries and their location relative to each other. The only accurate representation is a true globe. The surface of the Earth is non-Euclidean and thus the rules of geometry that you’re used to don’t apply: parallel lines will eventually meet (e.g. lines of longitude meeting at the poles) and the angles inside a triangle can add up to more than 180°.

The shortest distance between two points, regardless of geometry is called a geodesic: on  flat 2-dimensional planes geodesics are straight lines and on the surface of 3-dimensional spheres geodesics are curved.