Identification of a nuclear explosion uses a number of different methods. The Comprehensive Test Ban Treaty Organisation (CTBTO) runs a series of networks which listen for infrasound sound waves produced in the atmosphere by above-ground explosions; which monitor the oceans for underwater tests; and which monitor seismic activity to detect underground tests. The CTBTO also run a network of radionuclide sensors that sample the air to detect certain isotopes produced by nuclear explosions.
But if a nuclear weapon is ever used again as a weapon of war, the first notification will come from space-based networks (e.g. the US DSP or the Russian Oko) looking for the characteristic double flash of a nuclear detonation.
Watch the video above of the first two seconds of the Castle Bravo nuclear test. Do you notice anything unusual? Let’s take a look at a few individual frames.
Frame 01
Frame 11
Frame 49
The explosion begins bright, but then dims before becoming bright again: this is the nuclear double flash. It’s a little easier to see in the slowed-down excerpt below.
The variation in the brightness of the light emitted by a nuclear explosion follows a distinct pattern. It is possible to build light sources that are as powerful as nuclear explosions, or to produce light sources that have the same double flash characteristics, but not to produce a source with both characteristics. Thus the nuclear double flash is taken as irrefutable evidence that a nuclear explosion has taken place.
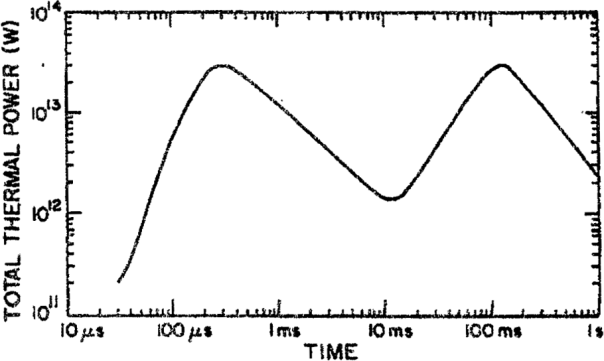
Note the logarithmic scale on both axes.*
As the nuclear explosion begins, the bomb and all of its components are heated to extremely high temperatures of around ten million kelvin. This causes these components to emit low-energy (“soft”) x-rays and high-energy (“hard”) ultraviolet waves. These x-rays and UV waves are absorbed by the air within a few metres of the device and this causes the air to be heated to temperatures of around one million kelvin, causing it to become incandescent and emit light. This is responsible for the initial, very fast (about three hundred millionths of a second after detonation) bright peak.
At the same time, the explosive shock wave itself (the hydrodynamic front) is expanding outwards and quickly compresses the air in front of it like a piston, causing it to become superheated. Inside this shock wave, the temperature is so high that the gas inside it become completely ionised (i.e. the gas becomes a plasma) and this makes the shock wave opaque to light. The brightness minimum is therefore caused by the shock wave “trapping” light behind it as it forms.
Light is still emitted because the shock wave itself is incandescent and is therefore emitting light outwards, ahead of itself, but this light is about one-tenth of the brightness of the preceding and following maxima. As the shock wave expands, it cools rapidly, and as it cools it becomes more transparent, allowing the light previously trapped behind it to escape. This is responsible for the second bright peak, which lasts much longer than the first because the full energy of the weapon is now being fully released, with nothing to block it. As the fireball expands it dissipates, and this is responsible for the gradual decrease in brightness.
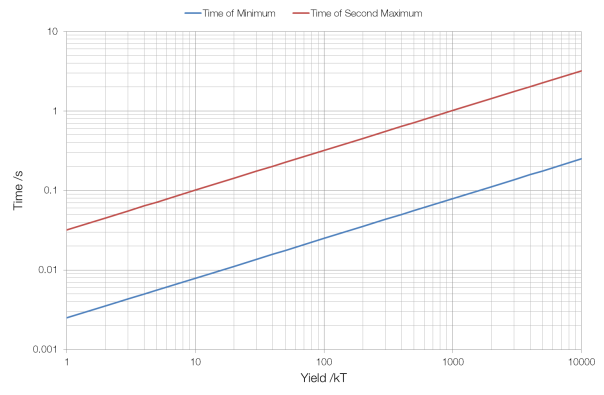
As the graph above shows, the time of the first minimum and the time of the second maximum depend on the weapon’s yield. A larger yield means a more powerful initial release of energy, and a more powerful shock wave, and this shock wave then takes more time to “pass through” the initial hot region created by x-ray/UV absorption, and then also takes longer to cool down to the point at which is becomes transparent to the light that it has trapped behind it.
For a one kiloton device, the time between the minimum and the second maximum is only 30 milliseconds, too short a gap for the human eye to perceive, but bhangmeters aboard satellites can spot it (and by measuring the time interval get a rough idea of the weapon’s yield). For larger weapons, such as the 100 kT warheads aboard the UK’s Trident II D-5 missiles, the interval is long enough (0.3 seconds at 100 kT) for human beings to perceive.
* Taken from Guy E. Barasch, “Light Flash Produced by an Atmospheric Nuclear Explosion”, LASL-79-84, Los Alamos National Laboratory, 1979.