The simplest answer to the question of whether your weight changes when you ride in a lift is ‘no’. Your weight, being the force with which the Earth pulls down upon you due to gravity, does not vary with speed or acceleration.
It does, however, feel like your weight changes when you ride in a lift. Because your weight is the force between you and the Earth (and between the Earth and you) you cannot actually feel your own weight; what you feel is the ground pushing up against you (the normal reaction force). Because of Newton’s Third Law (“each force has an equal but opposite reaction force”) this force is equal to your weight pushing down on the Earth.
When the lift accelerates and decelerates the force that the cables and motors exert on the lift is either added to, or subtracted from, the force with which the floor of the lift pushes up on you. This is what makes you feel heavier and lighter.
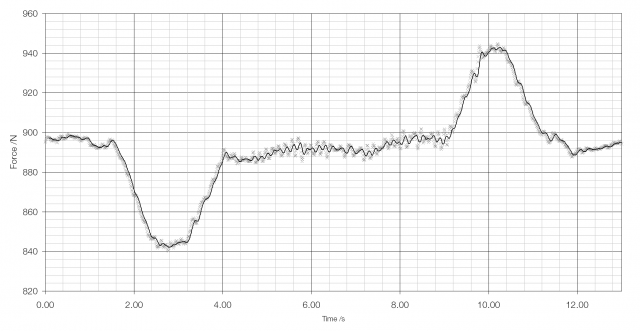I used a PASCO force platform and a SPARK datalogger to measure the apparent change in my weight as I rode downwards in a lift.
You can see a drop in apparent weight as the lift accelerates downwards, this then returns to normal as the lift travels at constant speed before rising again as the lift decelerates. By measuring the peak forces and using Newton’s Second Law of Motion I can calculate some approximate values for the maximum acceleration and deceleration of the lift in question: for the lift at school these values were 0.569 m/s2 and −0.625 m/s2, showing the lift decelerates at a significantly higher rate than it accelerates.
Were you in a lift that was accelerating downwards at the same rate as gravity (9.81 metres per second per second) you would feel weightless; were you in a lift that was accelerating upwards at the same rate you would feel like you weighed twice as much.
Do you not think that for ‘weight’ to be consistent with ‘weightlessness’, such as for astronauts, it has to mean the reaction force on an object in a gravitational field? This is how Walter Lewin teaches it at MIT.
Mach’s philosophical works changed Einstein’s ideas about physics so that he framed gravitation around observers, not perceived paths. He came to the realization that free-fall observers are inertial observers because they don’t a *feel* a force. The rest was to figure out what it seems they are accelerating, for an outside observer’s point of view.
I don’t think astronauts (at least those in LEO) are weightless at all. For me, for someone to be truly weightless (as opposed to apparent weightlessness) the value of g in W=mg must be equal to zero and in LEO g?9. As much as I love Walter Lewin I guess I’d have to disagree with him on this.
Very nice representing skill
So if we measure our weight in a moving lift. Will it change or something?
No. It will feel like it does, but your weight depends only on your mass and the local gravitational field strength.