I’ve recently been experimenting with making spherical ice cubes for cocktails.

But why go to all the fuss of making spherical ice cubes? What’s wrong with regular ice cubes? The answer is surface area to volume ratio: the volume of the ice provides the cooling effect but the surface area controls how fast the ice melts – the lower the surface area to volume ratio the longer the ice will take to melt for the same cooling effect. Essentially, a lower surface area to volume ratio keeps your drink cold, but stops it from becoming too diluted.
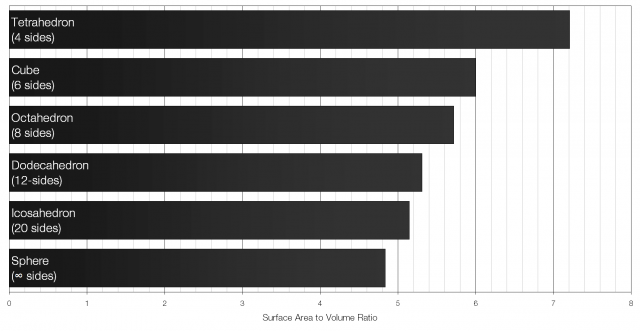
A cube with sides of length x will have a volume of x3 and a surface area of 6x2. The surface area to volume ratio for a cube is therefore 6 to 1 (6:1). Of all the Platonic solids (solids with identical faces) the icosahedron has the lowest surface area to volume ratio.

Of all the regular shapes a sphere has the lowest possible surface area to volume ratio. That is what makes it particularly well suited for cooling drinks.
The production of spherical ice cubes is also quite interesting. They’re usually made in an extremely elaborate process using large blocks of ice that are then shaped using metal “presses” (usually made of copper or aluminium as they are very good conductors of heat).
thanks! it helped me so much for my 6th grade science fair.
I once watched a barman in a cocktail bar in Tokyo sculpt his own spherical ice balls. He had a block of ice, a whiskey glass, and a chisel.
What would your opinion be of a skull-shaped ice ‘cube’ 3×3? Like the Gamago Skull Ice Cube
In shape a skull is closer to a sphere than a cube, so I think it’d be better than a cube, but not as good as a sphere.
Is there an explanation for why the volume of the ice provides the cooling effect? Because intuitively I think that it is the outside layer of cold ice atoms that cool the adjacent warmer atoms of the liquid.
Thanks helped a lot
@raviwoods think of “volume” as “supply”, and “surface area” as “time”. The more volume, the more time spent cooling something.
@op: I don’t think your calculations are correct for some things. E.g:
” A cube with sides of length x will have a volume of x3 and a surface area of 6×2. The surface area to volume ratio for a cube is therefore 6 to 1″
This isn’t correct, the ratio would be 6:1x, you’re forgetting a power. E.g., of length 2, the surface area is 24 units, but the volume would be 8 units (3:1, aka 6:2 or 6:1(2)). These ratios will always vary and you essentially need to use integration or some simple calculus to determine the points at which they have the lowest surface area to volume ratio. From there it’s a matter of choice.
Even spheres have this variance in ratios:
Volume(sphere): 4/3 pi * r^3
Surface Area(sphere): 4pi * r^2
Ratio:
4pi * r^2 : (4/3) * pi * r^3
r^2 : (1/3) * r^3
1 : (1/3) * r
Good news is, the bigger the sphere, the slower the melting in relative terms to volume.
This is absolute nonsense.
The surface area to volume ratio of a cube is not constant. Simple maths shows this. Work out for yourself the ratios for a cube with sides of length 30cm and then another with sides of length 20cm. For 30 cm the S.A:V ratio is 1:5. For 20cm it is 1:3.3 recurring.
Your error was to say x^3 was the same as x^2. And you got the ratio the wrong way round. Perhaps you need to water down your whisky more. Try smaller ice cubes; their S.A:V ratio is higher.
And I’m an English teacher…
The calculations are for a unit volume. I guess they don’t cover that in English.
Y cn’t xtrplt nt vlm nt gnrl rl.
” cb wth sds f lngth x wll hv vlm f x3 nd srfc r f 6×2. Th srfc r t vlm rt fr cb s thrfr 6 t 1 (6:1)”
Th S.:V rt f tht prtclr cb s 6:1, bt nt f ny thr cbs. S Gll’s sqr-cb lw. Ths shld b yr brd nd bttr.
A unit volume would imply they all have the same volume. They don’t. You are doing the calcs with a unit length. As several have said, the SA/V ratio changes with size.
Cube 1 side = 2
SA / V = 2x2x6/(2x2x2) = 3
Cube 2, side = 1
SA / V = 1x1x6 / (1x1x1) = 6
So the SA/V is not constant.
” cb wth sds f lngth x wll hv vlm f x3 nd srfc r f 6×2. Th srfc r t vlm rt fr cb s thrfr 6 t 1 (6:1).”
Frst sntnc: crrct
Scnd sntnc: bsrd
Y cn’t xtrplt nt vlm nt gnrl rl f cb t sqr rts. thnk y jst nd t dmt y md bsc rrr. W cn ll mv n thn!
cb wth sds f lngth x wll hv vlm f x3 nd srfc r f 6×2. Th srfc r t vlm rt fr cb s thrfr 6 t 1 (6:1).
Frst sntnc: crrct
Scnd sntnc: bsrd
What?
You’ve got the science wrong. Chilling the drink requires dilution. The faster the ice melts, the faster the drink cools down. Once the drink is sufficiently cold, the speed of the melting slows down correspondingly. Spherical ice cubes are used because they look cool, not because they melt more slowly.
Nope.
Heat transfer rate is proportional to the heat transfer surface. By lowering surface area, you are slowing the cooling effect. The ice melts more slowly, but the drink cools more slowly too.
Neglecting heat lost to the environment, the amount of ice (total volume) that melts is fixed for a given change in temperature of the system (conservation of energy). The speed at which the cooling takes place is a function of the mechanism of heat transfer (convection, conduction, radiation), the heat transfer surface, and the thermal conductivity of the materials involved. Lower the surface, lower the cooling rate.
Did you read the article, Anonymous? It doesn’t look like you did.
Ths s th mst stpd rtcl ‘v vr rd, nd “Mr Rd” clrly knws nthng bt physcs, mths r nglsh. H s ls dckhd.
This is a great idea. Kepp being cool. slay all day!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!