Tag Archives: thermodynamics

Why Can’t We Get to Absolute Zero?

,

The temperature of a substance is a measure of the average kinetic energy of the particles in that substance. As the average kinetic energy of the particles increases (i.e. they move faster), the temperature of that substance increases.

Some of the particles in a very hot substance will be moving slower than some of the particles in a very cold substance, but the average speed of the particles in a hot substance will be faster than the average speed of the particles in a cold substance. The number of particles at each speed in a gas is governed by something called a Maxwell-Boltzmann distribution, and is shown for air in the graph below:

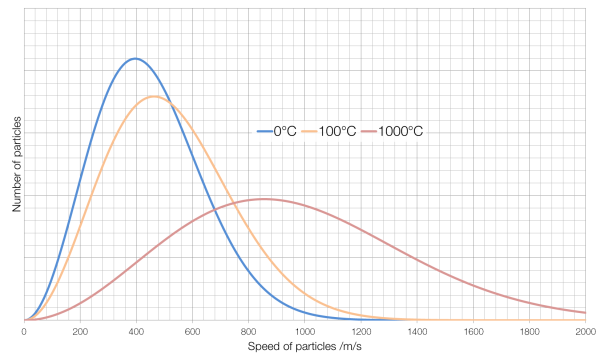
air-maxwell-boltzmann

The average speed for particles of air* at 0°C is around 400 metres per second, for air at 100°C it is about 460?m/s and for air at 1000°C it is about 860?m/s. (Note also that at 1000°C there is far more variation in the speeds of particles than for air at 0°C.) At absolute zero, the coldest possible temperature, particles have a minimum of kinetic energy, and therefore the lowest possible speed. (They cannot have a kinetic energy of zero and actually be stationary because of something called degeneracy pressure.)

So why can’t we cool something all the way to absolute zero?

For something to cool down, it has to lose thermal energy. In order to lose thermal energy, this thermal energy has to go somewhere, and thermal energy only ever moves from hot to cold.** For example: a warm can of drink placed into a cold fridge loses thermal energy to its surroundings until it reaches the same temperature as the fridge’s interior.

Therefore, in order to bring something to absolute zero it would have to be surrounded by something that is colder than absolute zero, and this is impossible: hence you cannot achieve a temperature of absolute zero.

The closest we’ve ever got to absolute zero is less than 100 picokelvin, or 100 trillionths of a degree above absolute zero at the Low Temperature Lab at the University of Aalto in Finland. Interestingly though, it would be possible for something to feel colder than absolute zero due to wind chill.

* Obviously air is made up of different gases travelling at different speeds, so this is an average, weighted by the masses and prevalences of the different gases that make up air.

** It would actually be more accurate to say that the net movement of thermal energy is always from hot to cold. Some energy may go from cold to hot, but more will always go in the opposite “direction”.

Cooling towers

,

cooling-towers

A pair of metal cooling towers at a power station in the Ukraine.

Cooling towers are an essential part of many power stations. Although they are most commonly associated with nuclear power stations, they are found in any power station that uses heat from burning fuel to generate electricity. (Drax, a coal-fired power station that is the largest in Western Europe at 3960 megawatts has twelve cooling towers.)

An aerial view of Drax coal-fired power station.

The purpose of a cooling tower is to extract waste heat from the power station so that the working fluid (water) can be reused. This waste heat passes into cold water, heating it in the process, and this warm water is then fed into the cooling tower where it cools and is then reused. The separation of the working fluid (purple and blue) and the waste heat extraction (grey pipes) is obvious in the diagram below.

cooling-tower-diagram

The space below the water inlet is filled with a material designed to increase the surface area of the water in contact with the air, helping to speed up the process of heat loss.

fill-plates

Fill plates mounted underneath the outlet nozzles.

The hyperboloid shape of cooling towers ensures continuous non-turbulent airflow, maximising the amount of air per unit time moving through the tower. Air enters at the bottom of the tower and accelerates up the tower as it is heated by the warm water, drawing fresh cool air in at the bottom due to the stack effect. In the photograph of a disused cooling tower below, the spaces at the bottom of the tower through which air enters are clearly visible.

inside-cooling-tower

Source: Tom Blackwell

Tog

, ,

Duvets are often rated by their “tog” rating. But what is tog?

Tog is a measure of a duvet’s thermal resistance. It measures the extent to which the duvet resists the transfer of thermal energy through it. One tog is equal to one-tenth of a metre squared kelvin per watt or 0.1 m²K/W. Thermal resistance can be a bit difficult to understand, but the reciprocal of thermal resistance, the thermal conductance, is a bit easier to grasp.

A one tog duvet would have a thermal resistance of 0.1 m²K/W and a thermal conductance of 10 W/m²K, a two tog duvet would have a thermal resistance of 0.2 m²K/W and a thermal conductance of 5 W/m²K, and so on.

A lightweight summer duvet* has a tog rating of about four, so its thermal conductance is 2.5 W/m²K. This means that 2.5 watts of thermal energy will move through each square metre of the duvet for every one kelvin difference in temperature between the sides of the duvet.

Whilst sleeping the average person puts out about seventy watts of heat. Some of this heat will be radiated into the mattress, and some will leak out around the head and neck and edges of the duvet, but it’s not unreasonable to think that around fifty watts is going into the air surrounding the body underneath the duvet.

To maintain a constant temperature underneath the duvet the amount of heat lost must be equal to the amount of heat output by the body. If an eight tog (1.25 W/m²K) autumn duvet has an area of three square metres then this break-even point will be reached when the difference in temperature between the two sides is about thirteen degrees (50 ÷ (3 × 1.25)). Given a skin temperature of 35°C this duvet will therefore keep you at a constant temperature in a room at a temperature of 22°C. If the room is colder than 22°C then the air underneath the duvet will gradually cool down and the body will increase its rate of heat production to compensate. If the room is hotter than 22°C then the air around the body will continue to increase in temperature (until it reaches the same temperature as the body) making you uncomfortably hot and will probably cause you to throw off the duvet or stick your leg out from underneath the covers to increase the rate of heat loss.

If the duvet in the example above is replaced with a four tog summer duvet with a conductance of 2.5 W/m²K then the room would have to be a scorching 29°C, but it’s unlikely that in this situation you would want a constant temperature – you’d want to remain cool overnight. If it was replaced with a twelve tog winter duvet (conductance = 0.83 W/m²K) then the room could go down to 15°C before a net heat loss occurred.

All the calculations above are based on some unreasonable assumptions, the most obvious one being that heat is not lost throughout the whole three square metre surface of the duvet. If a person is “using” only half this area then the numbers involved change to reflect more realistic values: for a winter duvet the temperature difference required can be greater and for a summer duvet it can be smaller. The calculations also ignore the effect of any heat radiated into the mattress below the person and the insulating effect that this mattress would have.

* John Lewis classifies summer duvets as those rated at between three and four-and-a-half tog, spring/autumn duvets as those between seven and ten-and-a-half tog and winter duvets as those between twelve and thirteen-and-a-half tog.

Specific heat, latent heat and scalds

Why is being scalded by boiling steam so much worse for you than being scalded or burnt by a liquid or a solid at the same temperature?

The specific heat capacity of a material measures how much energy is required to change the temperature of that material. The specific heat capacity of water is 4180 joules per kilogram per kelvin, meaning that it requires 4180 joules of energy to raise the temperature of one kilogram of water by one kelvin.

The latent heat of a material is the energy required to change the state of a material without changing the material’s temperature. There are therefore two latent heats: the latent heat of fusion is the energy required to turn a solid to a liquid or vice versa, and the latent heat of vaporisation is the energy required to turn a liquid to a gas or vice versa. For water the latent heat of fusion is 334 000 joules per kilogram and the latent heat of vaporisation is 2 260 000 J/kg.

If a one gram drop of boiling water (at 100°C) falls on skin at a temperature of 35°C then the temperature of the water quickly falls by 65°C. To drop the temperature of one gram of water by 65°C requires a change in energy of 272 joules. Because heat always flows from a hotter body to a colder one* this heat flows into the skin, damaging skin cells as it does.

The situation is different if one gram of boiling steam (still at 100°C) hits the skin. First it has to change state into water, and then cool down just as above. In the process of changing state from a gas at 100°C to water at 100°C it releases a huge amount of energy: an additional 2260 joules when compared with the 272 joules released as it cools. If we assume that the severity of the scald is proportional to the energy released (which is a very reasonable assumption) then a scald with boiling steam does 931% of the damage that a scald with boiling water does.

The graph above shows how the temperature of a 1kg block of ice at −100°C changes as energy is supplied to it. The horizontal sections occur when energy is being absorbed but the temperature of the substance is not changing; this is because the energy is being used to weaken bonds between molecules as the state changes first from solid to liquid and then from liquid to gas. The longer horizontal section in the liquid-gas state change indicates that more energy is required to turn water into steam than is required to turn ice into water. This is reflective of the relative strengths of the intermolecular bonds in solids, liquids and gases. The differing gradients of the sloped sections reflects the fact that the specific heat capacity of water varies with state.†

* More accurately, the net flow of heat is always from a hotter body to a colder one.

† For the sake of simplicity, the specific heat capacity of water in each state has been assumed not to vary.

Liquid cooling

, ,

Computer hardware produces a huge amount of heat when operating. Usually this heat is removed by a combination of heatsinks and fans

The grey heatsink conducts the heat away from the processor and the sink’s fins give the heatsink a larger surface area for the air moved by the fan to blow over. Some computers use very large heatsinks in order to do away with the need for a fan entirely, relying only on natural convection currents for cooling.

Some computers do away with fans by pumping water past the heatsink; water is a much better absorber of heat than air* and therefore the system uses less power for cooling.

Green Revolution Cooling have gone one step further – they actually submerge the computing hardware in a special non-conductive liquid. This liquid then circulates, transferring the heat away to an external evaporation tower.

They claim that their cooling system will pay for itself within 1-3 years.

* The specific heat capacity of air is 1.007 joules per gram per kelvin and the specific heat capacity of water is 4.187 J/g/K. This means that water will absorb more than four times the energy of the same amount of air for the same increase in temperature. Green Revolution don’t say what the specific heat capacity of the fluid they use is, but it’s likely to be greater than water’s.