Sound is created by vibrating objects. As an object, such as a loudspeaker’s diaphragm moves back and forth it compresses the air, causing changes in pressure. These changes in pressure cause your eardrum to move back and forth and these back-and-forth movements are translated by your brain into sound. Larger, louder, movements cause greater changes in pressure.
 A tuning fork creates compressions (higher pressures) and rarefactions (lower pressures) in the air.
A tuning fork creates compressions (higher pressures) and rarefactions (lower pressures) in the air.
The human ear is incredibly good at detecting changes in air pressure; it can detect the greatest range of stimuli of all your senses. The quietest sound that the ear can hear is the smallest change in pressure that it can detect: 20 µPa, less than a billionth of atmospheric pressure. To calculate the volume of a sound you must compare the pressure change caused by the sound with this smallest detectable change.
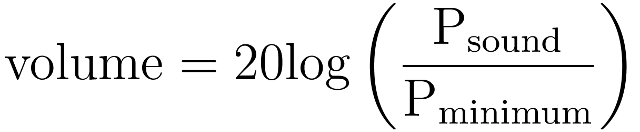
The decibel* scale is logarithmic. One bel represents a tenfold increase in pressure so a 50 dB sound is ten times louder than a 40 dB sound. The average volume of human speech is about 60 dB and the threshold of ear pain is 130 dB, some 107 or ten million times louder.
Because a sound wave consists of alternating low and high pressures there comes a point at which the sound is so loud that the rarefaction (low) pressure is the lowest possible pressure: a vacuum at 0 Pa. This corresponds to a compression pressure of one atmosphere or 101325 Pa. If we put these figures into the equation for volume we find:
![]()
So there you have it: the loudest possible sound is 194 dB. It has often been said that the loudest ever recorded sound was the eruption of Krakatoa in 1883 which was heard from nearly 5000 km away. The pressure wave created by the eruption was measured to be at least 20000 Pa, equivalent to a volume of 180 dB, 101.4 or twenty-five times quieter than the loudest possible sound.
* The prefix deci- indicates a tenth.
Your analysis is incorrect. It is possible to get an overpressure of more than 1 atmosphere, without ever going to “negative pressure” which is indeed a curious concept that I doubt we will do in any macroscopic device.
There are a couple of issues. Over 140dB SPL or so, the whole idea of linearity in atmospheric transmission of sound falls pretty much completely apart, for instance. Air is, strictly speaking, a linear medium for sound waves only at zero intensity, but in fact nonlinearities do not start to show up until in the 90dB range, become pretty obvious at 120dB if you’re looking, and the whole idea of linearity starts to fall apart at 140dB (all dB SPL, of course, unweighted).
A point you might want to make is that the brownian motion at the eardrum creates a white noise (20Hz to 20kHz) level of about +6dB SPL (which you can’t hear because there is too little energy in any one ERB or Critical Band). There is, therefore, a limit at low levels, as well.
All in all, you might want to make the point that the sound pressure we are designed to process is from about 2×10^-10 atmosphere to about 10^-5 atmosphere. That’s from 0 dB SPL to 94dB SPL.
It is absolutely possible to get an overpressure of more than 1 atmosphere, but then you’re not dealing with a sound wave anymore, but rather a shock wave.
how about for the loudest noise ever the moon as we know it crashing in to earth as you can tell the would be all most unbeat.
This is quite wrong… compare to other professional websites…
I beg to differ.
I would simply nit-pick in saying that “it’s the loudest sound possible” only at standard atmospheric pressure :)
On Venus, on the other hand, you could have MUCH louder sounds without it being a shock wave (and on Mars, it’d probably be impossible to have anything even approaching normal conversational levels.)
So what about sound in other mediums such as water for example?
Interesting question. I don’t think it would make any difference. Anything over 194 dB is more accurately described as a shock wave rather than a sound wave.
Ambient pressure at a point in either our atmosphere or water varies based on depth.
As water is much denser than the atmosphere, pressure increases quickly. At 10m, ambient pressure is twice what it is on land.
Calculating based on the pressure at the bottom of the Mariana Trench (8.338×10^7 pascals), the maximum sound volume ends up being 581dB – astronomically loud in comparison with the loudest sound possible in air. You’d need an enormous amount of energy to generate such a sound though!
do we have the means to create a 194dB sound, or can it only happen in an event similar to Krakatoa?
I don’t think we could create a sound this loud, no. The energy and power required are too high.
Yr ntntn my b rght, ccrdng t yr wn stpd clssfctn. Bt y smply cnnt sy 194 dB s th ldst snd bcs vrythng bv t s clld shck wvs.
fghtr jt cn brch snd brrr vry sly, fly t Mch 2 r 3, y wld hr shck tht s rtd bv 1 br (r 0.1 MP) nd brst yr rdrms, f y r cls ngh. Cn’t s yr wn dfntns t sprd hlf nfrmtn.
SPL n wtr s whl dffrnt ss dlng wth dffrnt rfrnc prssr f 1 mcr pscl nd snrs, rgns vry sly prtng bv 250 t 260 dB r 1 mcrpscl t 1 m dstnc.
Nn-lnr prpgtn f ltrsnc sgnls n wtr ndr hgh-mpltd cstc cvttn chvs 300 kP (zr-t-pk) ndrwtr sng smpl trnsdcrs.
I do not agree to 194 dB at vacuum when you talk about a sound wave/pure ton/sinus.
dB is a comparison between different energy values and for a tone the RMS value should be used. At 194 dB the RMS value is 1 bar (100 000 Pa, 1 atm is ~1.013 bar). That means that the peak value is 3 dB higher or the min value will be below 0 Pa.
191 dB is the theoretical maximum sound pressure level for a ton if you ignore the nonlinearities close to vacuum.
A vacuum or a pressure dip to zero Pa shouldn’t be expressed in dB.
0 Pa in dB correspond to ‘minus infinity’ dB, for any referenced used.
“One bel represents a tenfold increase in pressure” ? Should be a tenfold increase in energy and sqrt(10)=~3.16 increase of pressure.