Tag Archives: computerscience

RAID Types

,

In computer science, RAID stands for Redundant Array of Independent (or Inexpensive) Disks. A RAID array takes multiple hard drives and treats them as one logical volume – the computer’s BIOS causes your operating system to treat an array of different drives as one single drive.

RAID 0

In RAID 0 data is split across two drives at the block level, in a process called striping. That is, the first part of a file is stored on Drive 1, the second on Drive 2, the third on Drive 1, the fourth on Drive 2, and so on. It offers no redundancy, so if one drive fails the data on both drives is lost, but it does offer improvements in terms of performance. Data can be read and written faster than with one single drive as the first part of a file can be read/written from Drive 1 at the same time as the second part is being read/written from Drive 2.

RAID 0 is most commonly used with two drives of the same size, as the size of the combined volume is limited to twice the size of the smallest drive.

RAID 1

In a RAID 1 setup the data is mirrored on each drive: every block of every file is written identically to each drive (i.e. the data is not striped). This offers the same performance boost as in RAID 0 when reading data, but writing data has to take place on every drive, so is limited by the slowest drive. RAID 1 offers redundancy in that if one drive fails, the data can be recovered from the other still-functioning drives in the array.

RAID 1 is also most commonly used with two drives, but any number of drives can be used in theory. However, there is usually little advantage to this, as it is highly unlikely that more than one drive would fail simultaneously.

RAID 2, RAID 3, RAID 4

RAID 2, RAID 3 and RAID 4 are modifications of RAID 1, but are now obsolete and not commonly used. They stripe data at the bit (RAID 2), byte (RAID 3) or block (RAID 4) level, and also include parity data, which is explained below.

RAID 5

A RAID 5 array must consist of at least three drives. Data is striped across n-1 drives, where n is the number of drives, and parity data (explained below) is stored on the final drive. Thus an array of  n identically sized drives yields a combined volume n-1 times the size of each drive, with the striping providing improved performance and the parity data providing redundancy. Parity data is spread out across all drives, which increases performance because during large file writing operations the RAID controller does not have to wait for a dedicated parity drive (as used in RAID 2, RAID 3 and RAID 4) to become available.

For a given file, blocks are stored on different drives and can therefore be read/written simultaneously, which offers some of the speed improvements of RAID 0 and RAID 1 (this also applies if the blocks of different files are located on different drives).

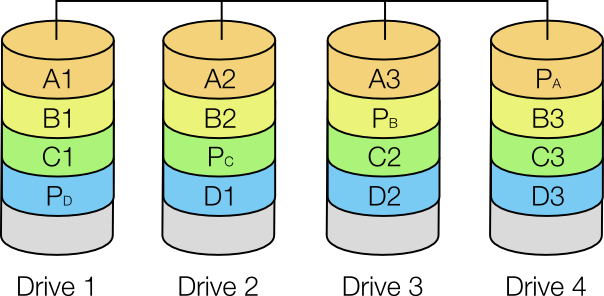
raid5

A diagram of a RAID 5 array using four drives.

Parity

For each series of bits parity is calculated by running an exclusive OR (XOR) on the data. An XOR takes individual bits and compares them: a 0 and 0 yields 0, a 0 and 1 or a 1 and 0 yield a 1, and a 1 and 1 yields a 0.

Imagine that we have two blocks of data: 10101010 and 11110000. These two blocks are stored on Drive 1 and Drive 2, and then the two blocks are XORed to yield the parity data which is stored on Drive 3.

Drive 1: 10101010
Drive 2: 11110000
Drive 3: 01011010

Now imagine Drive 2 fails:

Drive 1: 10101010
Drive 2: ????????
Drive 3: 01011010

We know to yield the first parity bit (0) the first bit of Drive 1 (1) must have been XORed with a 1; to yield the second parity bit (1) the bit on Drive 2 must have been a 1, and so on.  Thus we can reconstruct the missing data on a new Drive 2. We can also reconstruct missing parity data on a failed drive by simply repeating our original XOR process. However, if two of the three drives fail simultaneously, the data on the two failed drives is lost.

RAID 6

RAID 6 is similar to RAID 5, but distributes parity data across two drives, meaning that it can cope with two drives failing simultaneously and requires a minimum of four drives. RAID 6 is recommended in place of RAID 5 when using high capacity drives in large arrays, as rebuilding an array after a failure puts every other drive in the array under stress, which could cause a second drive to fail.

RAID 10 (aka RAID 1+0)

RAID 10 is  a nested array, combining striping and mirroring (and the advantages of both). In the minimal four-drive case, data is striped (RAID 0) between two mirrored (RAID 1) arrays. That is, the first block is mirrored on Drives 1 and 2, and the second block on Drives 3 and 4. A large RAID 10 array can sustain a large number of simultaneous drive failures, providing that no mirror loses all its drives (e.g. in the four-drive example above Drives 1 and 3, 2 and 3, 1 and 4 or 2 and 4 could fail and no data would be lost).

Other nested RAID arrays, such as RAID 50 (combining RAID 5 and RAID 0), or RAID 60 (combining RAID 6 and RAID 0) are also used. You can also use other configurations of drives, such as JBOD (Just a Bunch Of Disks), SPAN/BIG or MAID (Massive Array of Idle Drives).

Sorting Algorithms

Sorting lists of items into order is an important problem in computer science. What most people don’t realise is that there are many possible ways to do this.

Big O Notation

But before we look at individual algorithms, I need to explain big O notation. Big O notation is a measure of the efficiency or power of a particular algorithm. If an algorithm is O(n) then increasing the number of items to be sorted from 10 to 100 also increases the time taken by the same factor of ten. But if an algorithm is O(log(n)) then increasing the number of items to be sorted from 10 to 100 only doubles the time taken, as log(10) is 1 and log(100) is 2.

Bubble Sort

The bubble sort is the beginners sorting algorithm. It works by comparing each consecutive pair of items in the list and swapping them if they are the wrong way around.

Imagine that we are sorting the following six items: 536, 362, 653, 937, 351, 331.

The first operation compares 536 and 362 and because 362 is less than 536 the two items are swapped. The second operation compares 536 and 653, and because they are already the correct way around no swap takes place.

  1. 536, 362, 653, 937, 351, 331.
  2. 362, 536, 653, 351, 331, 937.
  3. 362, 536, 351, 331, 653, 937.
  4. 362, 351, 331, 536, 653, 937.
  5. 351, 331, 362, 536, 653, 937.
  6. 331, 351, 362, 536, 653, 937.

At this point, after five run-throughs and a total of ten swaps (but many more comparisons) the list is ordered.

The bubble sort is, on average, O(n2). This means that if the number of items increases by a factor of ten from 10 to 100 then the time taken increases by a factor of one hundred. The position of items in the list is particularly important in the bubble sort. Large items at the start of the list (rabbits) quickly move to the end of the list, but small items at the end of the list (turtles) take much longer to move to the correct position.

A modification of the bubble sort, known as the cocktail shaker sort, aims to reduce the effect of turtles by alternating direction on each run, running forwards and then backwards. For this reason it is sometimes known as the bidirectional bubble sort.

Running the list above through the cocktail shaker sort requires one fewer run than the bubble sort, because 331 acts as a turtle in the previous example:

  1. 536, 362, 653, 937, 351, 331.
  2. 362, 536, 653, 351, 331, 937.
  3. 331, 362, 536, 653, 351, 937.
  4. 331, 362, 536, 351, 653, 937.
  5. 331, 351, 362, 536, 653, 937.

Continue reading →

Disk drive sizes

,

In the International System of Units there are standard prefixes, based on powers of ten, used to indicate multiplication or division: kilo- to indicate multiplication by one thousand (103), mega- to indicate multiplication by one million (106), giga- to indicate multiplication by one billion (109), and so on.

But computer scientists don’t like powers of ten. The most basic unit of digital storage, the bit, is represented either as a one or a zero (with eight bits making a byte) and thus computer scientists are much happier working in binary, with powers of two rather than powers of ten. Standard binary prefixes do exist: kibi- for 210, mebi- for 220, gibi- for 230, etc.

SI Unit Size /B Binary Unit Size /B
kilobyte (kB) 1000 kibibyte (KiB) 1024
megabyte (MB) 1 000 000 mebibyte (MiB) 1 048 576
gigabyte (GB) 1 000 000 000 gibibyte (GiB) 1 073 741 824

The problem is that barely anyone uses the standard binary prefixes. During the “kilobyte era”, because 1000 and 1024 aren’t much different (2.4%) the difference was mostly ignored. But as file and hard disk drive (HDD) sizes have increased the difference between them has become more noticeable.

HDD manufacturers have stuck with SI (10x) sizes whilst operating systems calculate sizes in binary, but incorrectly use SI prefixes. A 256 gigabyte hard drive (i.e. one containing 256 billion bytes) will be reported by an operating system as being only 238 GB in size, a 6.9% difference. As HDDs becomes ever larger the problem will get worse: at the terabyte level the difference is 9.1% and at the petabyte level it is 11.2%.

Persuading operating systems to alter the way they report file sizes, thereby confusing users in the process, is unlikely to be a successful approach. A far better approach would be to persuade HDD manufacturers to change their marketing so that users purchasing a HDD receive the size they are expecting.*

* Though obviously, as a physicist, it causes me great mental anguish to abuse SI units in this fashion!