Most people assume that if you double the amount of radiation you double the damage caused, and that there is no threshold below which no damage is done. This is called the Linear No Threshold (LNT) model and is represented by the graph below: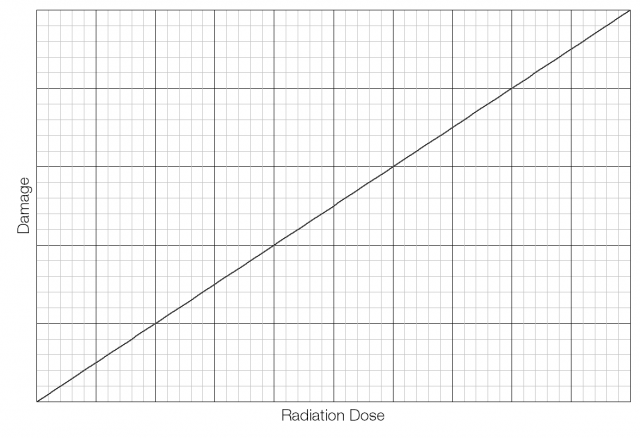

The LNT model has been the subject of some disagreement in recent years. The American Nuclear Society said in a 2001 Position Statement* that:

“There is substantial and convincing scientific evidence for health risks at high dose. Below 10 rem (which includes occupational and environmental exposures) risks of health effects are either too small to be observed or are non-existent.”

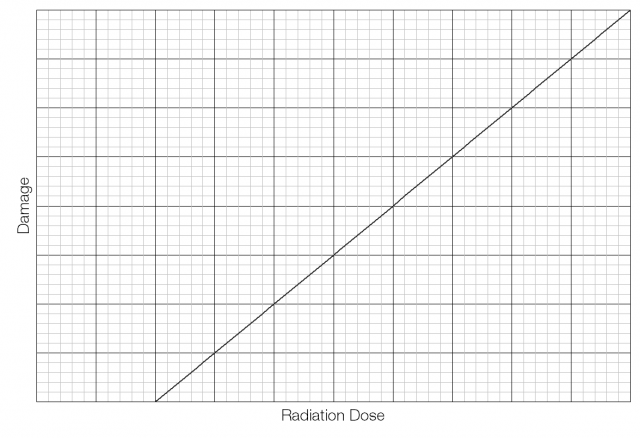
This linear threshold model holds that there is a limit below which no damage is caused, but that damage then increases linearly beyond that limit.

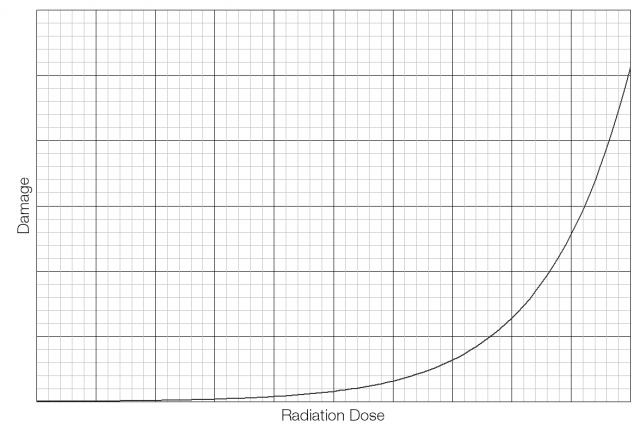
There are other possible models. Damage may increase in an exponential way, with very low damage at low doses but increasing amounts of damage at higher doses.

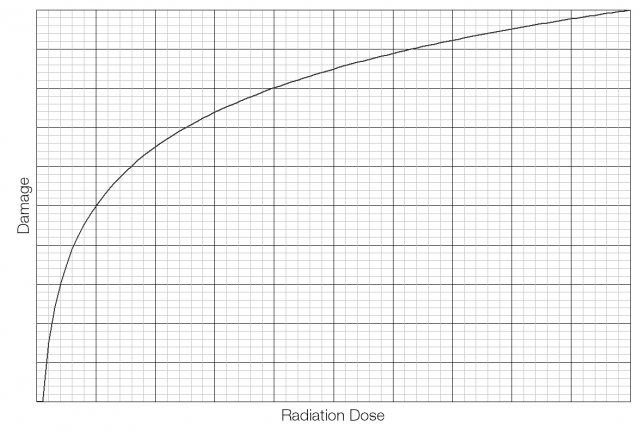
In a logarithmic model the damage would be very large at first, but taper off as the dose increases.

So which model is correct?

The LNT model remains the most commonly used by regulatory bodies, but there is growing interest in threshold models and in the idea of radiation hormesis, the idea that a small dose of radiation is actually good for the body by somehow stimulating the body’s repair systems. I think the most likely candidate is a J-shaped curve with a significant threshold but then a fairly rapid linear increase in damage caused.

* American Nuclear Society, Health Effects of Low-Level Radiation, Position Statement 2001.