The strength of the gravitational field at Earth’s surface g is 9.81 newtons per kilogram. This means that every kilogram of mass feels a force of 9.81 newtons pulling it downwards towards the centre of Earth.

As you climb higher and higher, the value of g becomes smaller and smaller. At the peak of Mount Everest, g?=?9.79?N/kg, and at the summit of Chimborazo, the farthest point from Earth’s centre, g?=?9.78?N/kg.

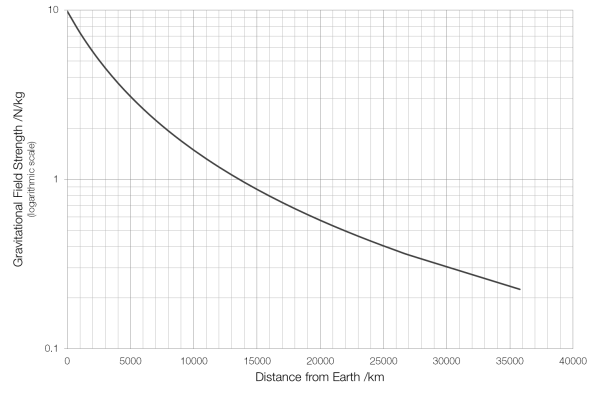
So what is the value of g aboard the International Space Station, in orbit around Earth? You would be forgiven for thinking that the answer is 0?N/kg, because the environment the astronauts are in is often described as “zero-g”, but this is not the case. The value of g aboard the ISS is actually 8.65?N/kg, only 12% less than on Earth’s surface.

An apple floats in mid-air aboard the ISS.

The astronauts aboard the ISS experience apparent weightlessness, not true weightlessness. The reason they appear to be in a zero-g environment is only because they are in orbit around the Earth – if the ISS were to slow to a halt it would fall towards Earth just like an object on Earth’s surface (though it’d fall a little bit slower at first).

In orbit the ISS is falling towards Earth at just the same rate as Earth is curving away, keeping it at a constant distance from Earth’s surface.* Because astronauts are in constant freefall they don’t push against the “floor” and the “floor” doesn’t push against them and therefore they feel weightless. If you’ve ever felt a little bit lighter in a lift as it started to move downwards, just imagine that effect taken to an extreme in a lift shaft where you can never hit the bottom.

Even geostationary satellites, like those that supply satellite TV, at a distance of 36000 km from Earth aren’t in zero-g. If they weren’t within Earth’s gravitational field they wouldn’t orbit and would fly off into space; for geostationary satellites g?=?0.224?N/kg.

The closest human beings have ever been to true zero-g is on the way to the Moon, at the point at which the gravitational pull of the Earth in one direction was equal to the gravitational pull of the Moon in the other direction. Because the mass of the Moon is about 1/81 of the mass of the Earth and the strength of a body’s gravitational field depends on the square of the distance from the body this point is about nine-tenths of the distance between the two: 346?000 km from Earth. At this point the pull from the Earth is 0.0032?g and the pull from the Moon is the same, but in the other direction.

* Imagine a giant cannon firing horizontally: too slow and the cannon ball will hit the ground, too quick and the cannon ball will fly off into space. But if the cannon fires at just the right speed the cannon ball will drop towards the ground at just the same rate as the ground curves away.