Monthly Archives: October 2011

Looking at constellations from a different angle

,

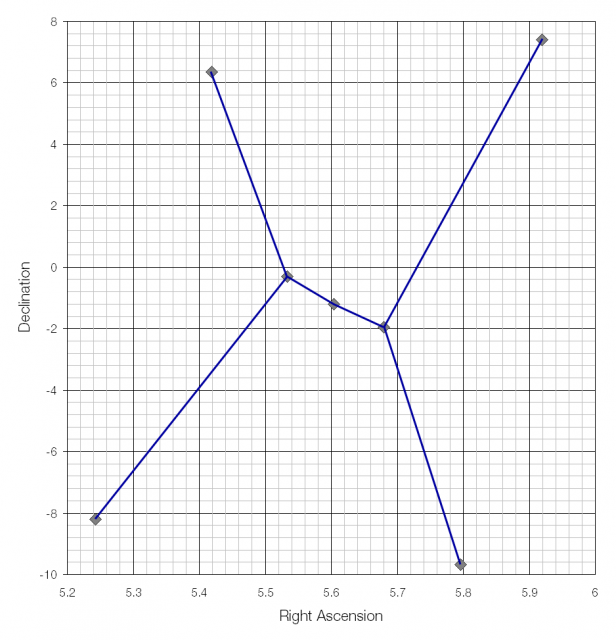
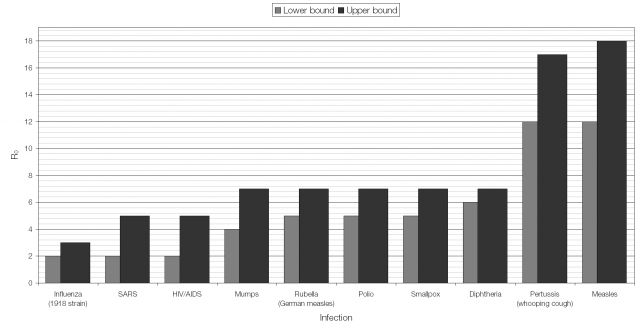
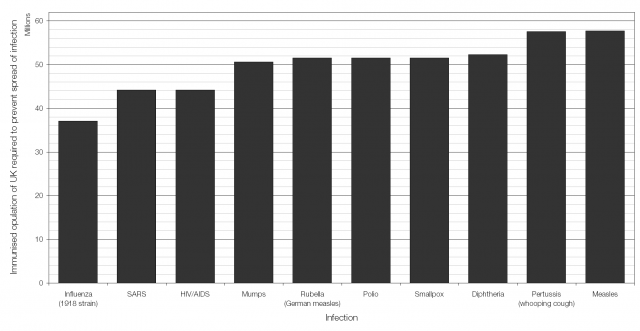
You are probably familiar with the constellation of Orion (The Hunter), in particular with the asterism that makes up Orion’s Belt.

Because of the way the right ascension data is plotted the images shown here are how they would appear to a distant observer looking at Orion towards Earth.

Because stars are so far away we tend to think of them as being painted onto a surface at a fixed distance – “like a huge picture painted on the sphere of the sky”. But if you look at the stars in three dimensions then Orion looks very different.

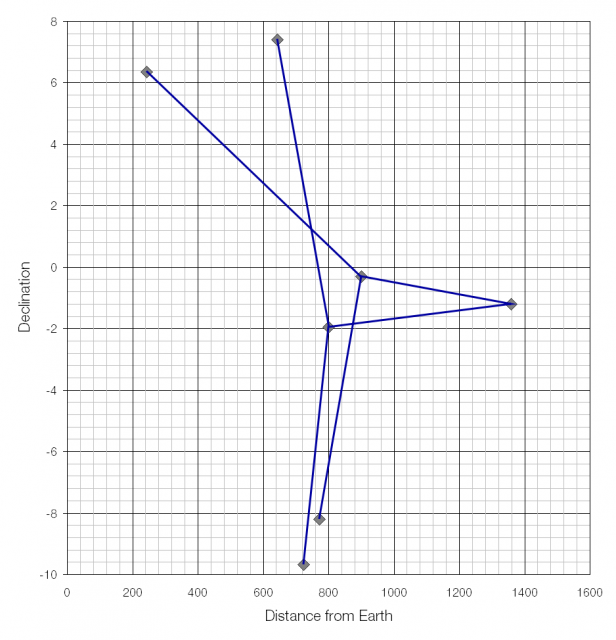
From above it’s difficult to recognise Orion’s shape as the lines connecting the two rightmost stars (Betelgeuse and Saiph) to the rightmost star of Orion’s belt (Alnitak) overlap:

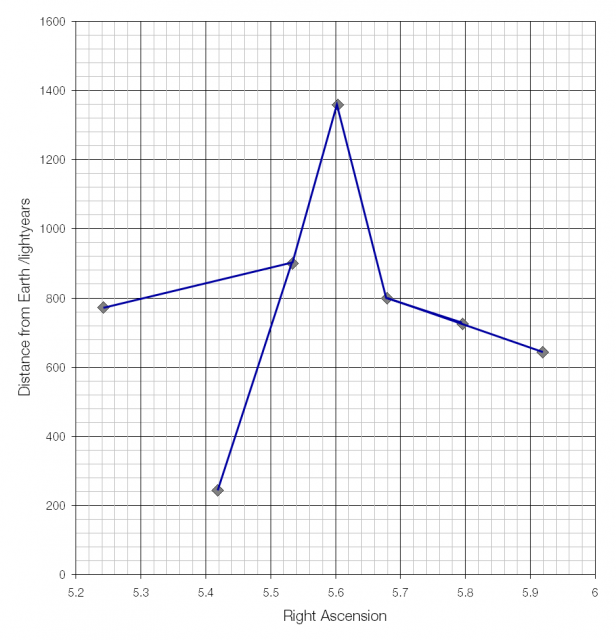
From the side the shape is more obvious. Alnilam, the middle star of Orion’s belt is by far the furthest star, more than 1300 light years away from Earth:

This post was inspired by an arXiv paper* by Dr Daniel Brown from the School of Science and Technology at Nottingham Trent University. You can download the data I used as an Excel spreadsheet (.XLS, 29 kB).

* Daniel Brown (2011) “The Orion constellation becomes installation: An innovative three dimensional teaching and learning environment”, arXiv:1110.3469v1 [physics.ed-ph].

Dating a common ancestor

,

Time Tree is a website that allows you to search for the point in time at which the genetic code of two organisms diverged; the time at which their last common ancestor lived.

Investigating human beings is quite fun: the last common ancestor that we shared with chimpanzees lived 6.3 million years ago and we shared an ancestor with gorillas 8.6 million years ago. We are much closer to cats and dogs (95.2 million years ago) than we are to ducks (292 million years ago).

If we start to look at more obviously different organisms we find much older most recent common ancestors: we shared an ancestor with jellyfish 892 million years ago and with the northern red oak tree 1.43 billion years ago.

It isn’t just humans that you can find the most recent common ancestors for. Horses and camels shared an ancestor 84.2 million years ago and cats and dogs a mere 55.7 million years ago.

R0

,

R0, also known as the basic reproduction number, is a measure of the ability of an infection to reproduce and spread in an unimmunised population. If R0 is less than one, each infected person infects (on average) less than one secondary person and the infection will die out. If R0 is greater than one then each infected person infects more than one secondary person and the infection will spread.

R0 varies greatly between diseases:

From the R0 figure the proportion of a population that must be immunised to prevent the spread of a disease can be calculated. If we use the population of the UK (61 838 154 according to 2009 figures from the World Bank) then we get the following graph:

You can see that for the most infectious disease on our list, measles, more than 93% (on average) of the population need to be immunised to prevent the disease from spreading (to prevent an epidemic). This is alarming in light of the failure of many parents to immunise their children due to unfounded fears about the MMR vaccine.

Spherical ice cubes and surface area to volume ratio

,

I’ve recently been experimenting with making spherical ice cubes for cocktails.

But why go to all the fuss of making spherical ice cubes? What’s wrong with regular ice cubes? The answer is surface area to volume ratio: the volume of the ice provides the cooling effect but the surface area controls how fast the ice melts – the lower the surface area to volume ratio the longer the ice will take to melt for the same cooling effect. Essentially, a lower surface area to volume ratio keeps your drink cold, but stops it from becoming too diluted.

A cube with sides of length x will have a volume of x3 and a surface area of 6x2. The surface area to volume ratio for a cube is therefore 6 to 1 (6:1). Of all the Platonic solids (solids with identical faces) the icosahedron has the lowest surface area to volume ratio.

Of all the regular shapes a sphere has the lowest possible surface area to volume ratio. That is what makes it particularly well suited for cooling drinks.

The production of spherical ice cubes is also quite interesting. They’re usually made in an extremely elaborate process using large blocks of ice that are then shaped using metal “presses” (usually made of copper or aluminium as they are very good conductors of heat).

Does your weight change in a lift?

, ,

The simplest answer to the question of whether your weight changes when you ride in a lift is ‘no’. Your weight, being the force with which the Earth pulls down upon you due to gravity, does not vary with speed or acceleration.

It does, however, feel like your weight changes when you ride in a lift. Because your weight is the force between you and the Earth (and between the Earth and you) you cannot actually feel your own weight; what you feel is the ground pushing up against you (the normal reaction force). Because of Newton’s Third Law (“each force has an equal but opposite reaction force”) this force is equal to your weight pushing down on the Earth.

When the lift accelerates and decelerates the force that the cables and motors exert on the lift is either added to, or subtracted from, the force with which the floor of the lift pushes up on you. This is what makes you feel heavier and lighter.

I used a PASCO force platform and a SPARK datalogger to measure the apparent change in my weight as I rode downwards in a lift.

You can see a drop in apparent weight as the lift accelerates downwards, this then returns to normal as the lift travels at constant speed before rising again as the lift decelerates. By measuring the peak forces and using Newton’s Second Law of Motion I can calculate some approximate values for the maximum acceleration and deceleration of the lift in question: for the lift at school these values were 0.569 m/s2 and −0.625 m/s2, showing the lift decelerates at a significantly higher rate than it accelerates.

Were you in a lift that was accelerating downwards at the same rate as gravity (9.81 metres per second per second) you would feel weightless; were you in a lift that was accelerating upwards at the same rate you would feel like you weighed twice as much.