Night vision

, ,

The vision of human beings is well-adapted to daylight; the human eye has evolved to see in the range of wavelengths that are brightest in the spectrum of light that the Sun emits.

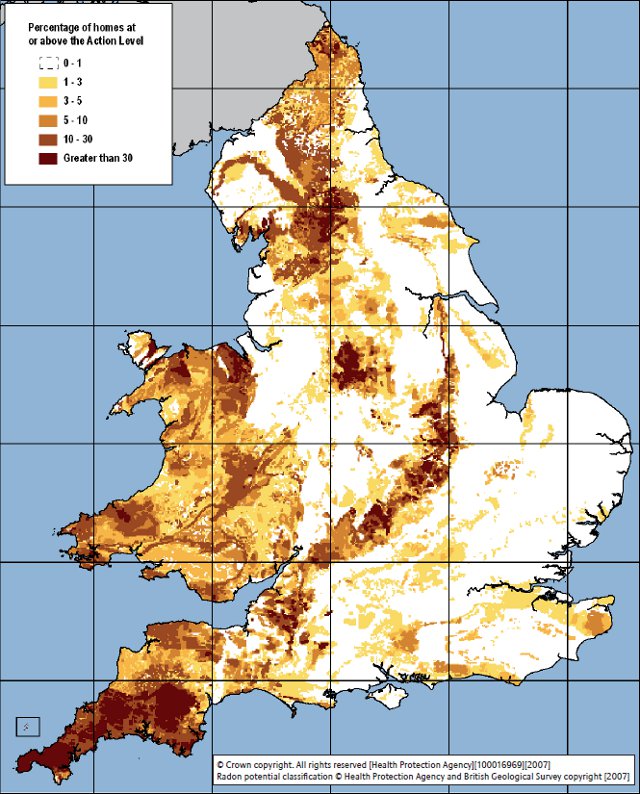
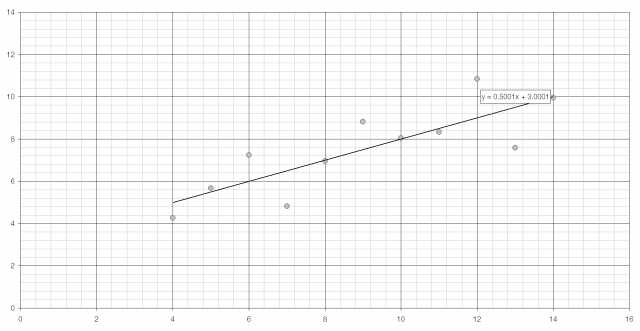
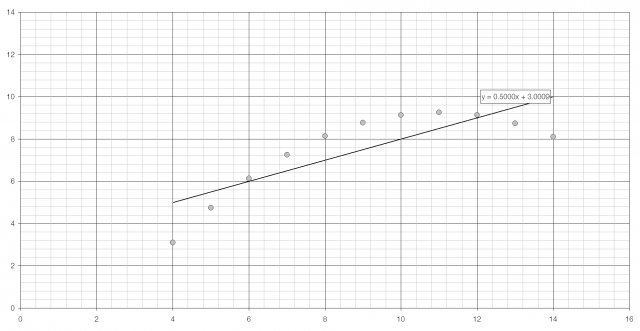
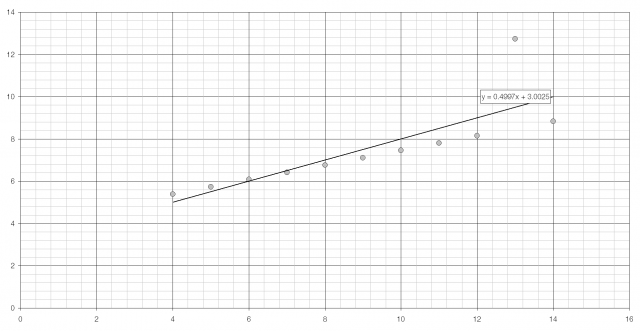
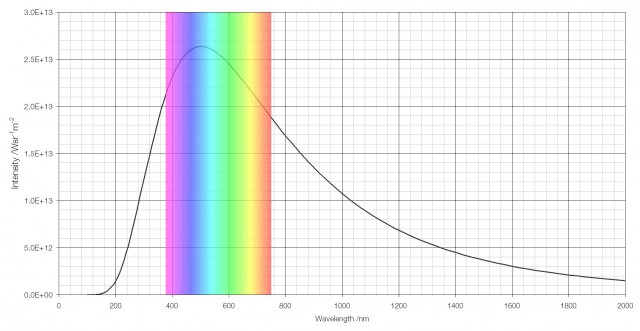The intensity of the light the Sun emits by wavelength, with the visible region highlighted.

But humans don’t see particularly well in the dark. The cones that are responsible for colour vision don’t function well at low light intensities, which is why night vision is almost entirely monochromatic – in the dark humans see in black and white.

When moving from bright light into darkness the first thing that happens to the eye is that the pupil dilates to allow in more light. The iris dilator muscle causes the pupil to increase in diameter by a factor of five (from 2 mm to 10 mm), increasing the amount of light entering the eye by about twenty-five (52) times, but this isn’t enough for true night vision.

The chemical rhodopsin that is present in the rod (brightness-sensing) cells is responsible for night vision. When exposed to light, rhodopsin immediately (within 200 femtoseconds*) splits to form a chemical called photorhodopsin, and then soon afterwards (within a few picoseconds) another chemical called bathorhodopsin.

The splitting of rhodopsin is accompanied by the formation of other chemicals called retinals, and during this splitting process a signal is sent down the optic nerve to the brain, registering the detection of light. (Retinal is created from vitamin A, and so people with a diet lacking in vitamin A frequently suffer from night blindness.)

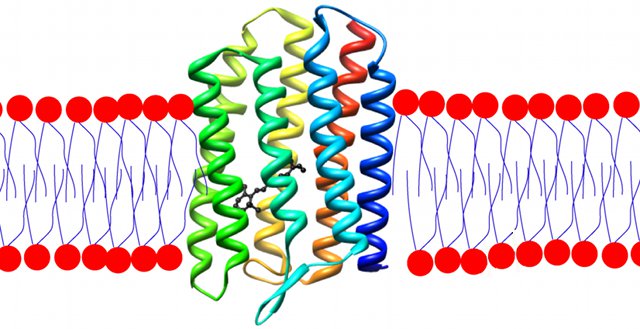
A molecule of rhodopsin (rainbow-coloured) embedded in a lipid bilayer.
A (black) retinal molecule is bound within the rhodopsin.

Over time, and at a consistent rate, the opsins and retinals recombine to form rhodopsin. If the eye is exposed to bright light all the rhodopsin splits at once (a process called photobleaching). When subsequently exposed to darkness there is therefore no rhodopsin to split and the eye cannot detect light properly. The person in question must wait for the rhodopsin to naturally recombine over time before proper vision can return, a process that takes between ten and thirty minutes to occur. When fully accustomed to the dark, the eye is between ten thousand and a million times more sensitive to light than previously.

The rhodopsin in human eyes is less-sensitive to red light than to other colours and therefore night vision is not particularly effected by red light. This is why red light is used in darkrooms and in aircraft before night-time parachute jumps.

Human eyes, unlike the eyes of many animals, do not have the tapetum lucidum which gives those animals superior night vision. The tapetum lucidum sits behind the retina and acts like a mirror, reflecting back photons of light that were not initially absorbed by the retina, giving the retina a “second chance” to detect the light. This improves their night vision and is what gives rise to the phenomenon of “eyeshine” often seen when taking photographs of animals.

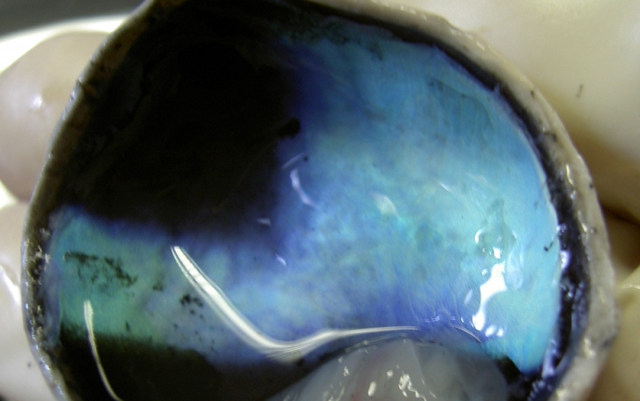
The tapetum lucidum seen in a dissected calf’s eye.

“Eyeshine” is very obvious in this photograph of a raccoon.

* Interestingly, the splitting of rhodopsin into photorhodopsin and retinal seems to be the fastest chemical reaction that has been directly studied.

The most radioactive parts of the UK

,

The average radioactive background dose in the UK is 2.7 millisieverts. Of this 2.7 mSv, 1.35 mSv comes from radioactive radon gas leaking out of the ground.

This radioactive radon (Rn-222) is produced by the decay of uranium-238, after a series of intermediate non-gas stages that cannot escape from rocks.

Because radon has such a large effect on the annual radiation dose that someone receives, it is closely monitored. In the UK, this monitoring is done by the Health Protection Agency (HPA). One of the things that the HPA does it produce radon maps, showing which areas of the UK have the highest presence of radon.

The map is graded by the percentage of homes in that area which have a level of radon beyond the action level of 200 becquerels per cubic metre (200 radon decays per second per cubic metre).

There are a number of important radon hotspots in the UK. The most noticeable one is Cornwall in the south-west where the average UK background dose is 7.8 mSv, nearly three times the national average. This is due to the presence of igneous granite, which naturally contains more uranium (10-20 parts per million) than other rocks.

Radioactive areas tend to be hilly, where igneous rocks have been forced to the surface or left behind by the erosion of softer sedimentary rocks (the Chiltern Hills are particularly radioactive, for example). The Yorkshire Dales sit on top of an underground deposit of pink granite called the Wensleydale Granite that lies underneath the Askrigg Block, and the Peak District features many granite outcroppings.

Biosphere lungs

,

Some people refer to the rainforests as “Earth’s lungs”. In reality this is quite far from the truth, as rainforests actually contribute little (net) oxygen to Earth’s atmosphere; 70% of oxygen production is done by water-bourne green algae and the cyanobacteria present in every habitat on Earth.

Biosphere 2, a sealed ecological system built in Arizona to study the interaction between different forms of life and as a test of the possibility of using closed systems in space colonisation, also had lungs.

Biosphere 2’s oxygen came from the facility’s six biomes: a 1900 square meter rainforest, an 850 square meter “ocean”, a 450 square meter mangrove wetland, a 1300 square meter savannah grassland, a 1400 square meter fog desert and a 2500 square meter agricultural system.

During the day the heat of the Arizona sun would cause the air inside the facility to expand. In order to avoid the large pressure difference that this would create (5000 Pa, or 5% of standard atmospheric pressure), Biosphere 2’s creators included two giant hemispherical “lungs”.

As the air inside the facility expanded it would flow through underground tunnels into the lungs. Each lung contained a large weight hanging from a rubber sheet; as the air expanded during the day the increased pressure would raise the weight into the air. In the evening, as the air cooled, the weight would pull the rubber sheet back down and push air back into the facility, thereby equalising any pressure difference as it appeared.

Source: lumierefl

William Dempster, “Biosphere 2 engineering design”, Ecological Engineering 13 (1999): 31-42 doi:10.1016/S0925-8574(98)00090-1 (.PDF).

Anscombe’s quartet

,

Anscombe’s quartet is four sets of data that are used to demonstrate the importance of graphing data.

Set 1 Set 2 Set 3 Set 4
x y x y x y x y
10 8.04 10 9.14 10 7.46 8 6.58
8 6.95 8 8.14 8 6.77 8 5.76
13 7.58 13 8.74 13 12.7 8 7.71
9 8.81 8 8.87 9 7.11 8 8.84
11 8.33 11 9.26 11 7.81 8 8.74
14 9.96 14 8.10 14 8.84 8 7.04
6 7.24 6 6.13 6 6.08 8 5.25
4 4.26 4 3.10 4 5.39 19 12.5
12 10.8 12 9.13 12 8.15 8 5.56
7 4.82 7 7.26 7 6.42 8 7.91
5 5.68 5 4.74 5 5.73 8 6.89
Mean 9 7.50 9 7.50 9 7.50 9 7.50
Variance 11 4.13 11 4.13 11 4.12 11 4.12
PMCC 0.82 0.82 0.82 0.82

Each set of data has near-identical statistical properties: the same average and variance (for both x and y), and the same product moment correlation coefficient and linear regression line. When plotted, however, they look entirely different. (The scale of the last graph is different from the others.)

You can download Anscombe’s quartet as an Excel spreadsheet.

Francis Anscombe, “Graphs in Statistical Analysis”, American Statistician 27(1) (1973): 17‑21. http://www.jstor.org/stable/2682899 (.PDF).

Haversine formula

,

The haversine formula is used to calculate the distance between two points on the Earth’s surface specified in longitude and latitude.

d is the distance between two points with longitude and latitude (ψ,φ) and r is the radius of the Earth.

As an example I have calculated the distance between Fermilab in Illinois (41° 49′ 55″ N, 88° 15′ 26″ W) and CERN’s Meyrin campus in Switzerland (46° 14′ 3″ N, 6° 3′ 10″ E). There’s a little too much maths for this site to handle so I have included a .PDF file of the working below.

The value calculated is 7084 km, which isn’t quite correct. This is because the formula assumes that the Earth is a perfect sphere when in fact it is an oblate spheroid. To compensate for this Vincenty’s Formulae must be used; these are much more complicated but give a more accurate value of 7103 km.