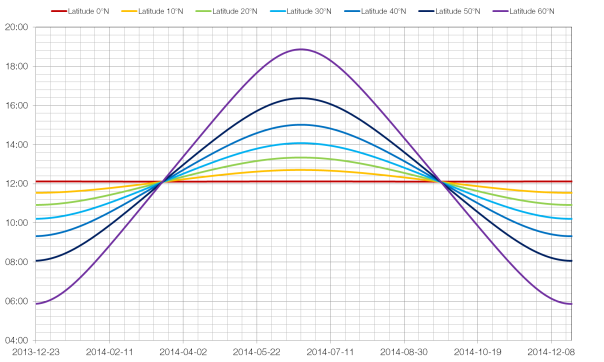
As the Earth moves around the Sun, the length of the day (defined as the time between sunrise and sunset) changes. The extent to which it changes depends on latitude, as shown in the graph below:
As you can see, the length of a day changes far more during the year at higher latitudes than at lower latitudes. (Latitudes beyond 66°33′ are not shown because the Sun does not always rise or set at these latitudes.) The graph runs from one winter solstice to the next, with the two equinoxes clearly visible in March and September.
It’s quite interesting to look at by how much the length of a day changes every day. This graph would have the same shape as the previous one, but not if we look at percentage change. In a way, this gives an impression of how quickly it appears that “the nights are drawing in”. 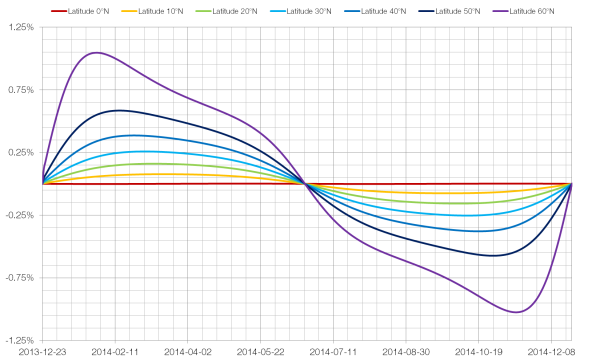
At higher latitudes the length of day changes quite noticeably in early January and mid-November. In some situations two adjacent days are different in length by nearly five minutes, and at some points the day loses nearly fourty minutes over the course of a single week.
OMG! I just got excited after seeing this post here. That sounds great to know statistically that what is the rate of change of day length with latitude. I’m thankful to you for making this informative post.
Thanks, always wanted to know this. But can you explain WHY the rate of change is faster either side of the winter solstice also the curious shape of the curve mid spring and mid autumn? Answer must be topological
I’m not sure I understand what you mean by “answer must be topological”?
Hi, I was finding your comment “It’s quite interesting to look at by how much the length of a day changes every day. This graph would have the same shape as the previous one” most confusing – because clearly when daylength is max/min, rate of change of daylength is close to zero – and at the equinoxes, rate of change is clearly max. In other words, the graph you allude to ought to be a graph of the first derivative, not an identical graph.
However, that equates to a sine/cosine situation ie: d/dx sin x = cos x – so it’s not the same graph but the same shape of curve moved along 1/4 year.
I think this could do with clearing up.
I’ve come up with two explanations for the asymmetry, one mathematical and one geometrical.
First, it’s a percentage change so it depends on the value and not just the rate of change (as would the first derivative) so an equal change in the length of day would be a greater percentage change near the winter solstice when the day length is smallest. This happens when the absolute change is small, which means the two effects are somewhat at odds, leading to the seemingly strange shape of the graph.
There’s also the fact that the sun is large enough for its light to not arrive at Earth perfectly parallel, so slightly more than half the planet is in daylight at any given time. So since (as an offset from 12 hours) summer days are longer than winter days are short (a careful inspection of the first graph reveals this) the percentagewise change will be even more perturbed.
The first effect is very dominant at higher latitudes. As an extreme example, above 70° in the Arctic the day-to-day percentage change in sunlight hours would be infinite (division by zero) with the first sunrise after a long winter with no daylight.
If there are other significant factors I’d be glad to hear them.
Can I edit that? Geometry is math. What I meant was arithmetic or algebraic reasons vs geometric.
This is interesting. The asymmetry of the 2nd graph is not intuitive. I think Toby provides an explanation. It would be helpful to have a graph of time delta, not as a percent, as well.
Um i can count to letter 5
Thank you. The exact graph I was looking for to show that at about the first week of February the sun speeds north and days lengthen at a quick and steady rate. Much more so than the previous weeks after winter solstice.
Is it a suitcase or a grocery bag?
Is it a grocery bag or a suitcase? I’ve been questioning my existence ever since I’ve thought of this question.
Regarding “impressions”: Note that aphelion and perihelion affect WHEN sunrise and sunset take place (in distinction to length of day). So in summer at the beach in Adelaide Sth Australia the sun sets at 8.33pm from 1st to 12th of January! Summer seems to last forever ?
But if you are a morning person it rises at 5:55am from 30th October to 13th November.
I am trying to find a good source of data for my students to create this graph on their own. I think I found one from NOAA.. but there is a lot of data to ignore. Do you have any suggestions? Looking for data on average temp changes also (by latitude)
I used the NOAA spreadsheet.
I’ve always said that the change of length of day is similar to the speed of a pendulum. Which I think is still true no matter where you are between 60 latitudes
Shouldn’t Earth’s tilt be a factor as well? Tilt for a latitude changes with seasons, so the equator never really truly experiences a perfect 12 hour day/night.
In your last paragraph you noted that;… ”At higher latitudes the length of day changes quite noticeably… etc.”
Why is this so? Why doesn’t the percentage stay the same? What are the reasons for differences, or length of time, given the same latitude? Does it have to do with our orbit not quite being a perfect circle?
Please use small words or provide other basic places for me to try and warp my mind around this. I can grasp most of it (other than the much needed math) but not all.
And by admitting this I’d hazard a guess I’ve answered my own question.
It’s to do with the fact that the Earth is tilted on its axis. When you are around the equator, it doesn’t make much of a difference what time of year it is.
Thank you Mr. Reed. Mentally going to the equator helped.
So my next question has to do with the rate of change of available light as time progresses.
I went out on the web in an effort to look for timetables to better illustrate what you said, as opposed to what I had been thinking, in an effort to better get a grasp on this.
I used this site: https://www.timeanddate.com/sun/usa/spokane?month=3&year=2020
and also one from the same place, for Kampala Uganda nearest the equator.
In comparing the two locations month by month, though not the exact year, of the lower graph to day by day times shown in the charts, it was easy to see Kampala hardly changed at all while here in Spokane (N. 47th.) it did so by seconds/day.
However the time gained at my northern latitude in our winter did not stay the same each day as it progressed over the next few months. Over time there was a an approximate increase of five seconds per day for weeks then began to change to lesser amounts until the equinox.
Your lower graph shows this ”distortion” (if I may) to the same degree. A soft bump shown to a greater degree the further north you go.
Why? Why isn’t it an even curve, an even amount of seconds, steadily gaining day after day.
Why doesn’t the amount of seconds gained, be a constant? What am I missing?
terry
This would be a good place to start: http://www.analemma.com/Pages/framesPage.html
Mr. Reid
Thank you. This was a bit of an ”ah-ha” moment for me.
Back on the 3rd I was getting close, but with no deeper thoughts on it other than to ask about the idea of our orbit not being a perfect circle. At that time I wasn’t able to make any further connections.
At the same time I couldn’t see any other ”parts” than what we have before us. We have the two round objects, one canted at 23.5 degrees and goes around the other.
It had to be simple, and that is what drove question after question. My wife is sick of listening as I bounce it off her and anyone else that would draw near.
A certain hell being curious.
You most likely hear from me again. Thanks so much for answering, AND in the same moment, giving me enough time and direction to wander down my own rabbit holes.
You’re a great teacher.
terry
Mr. Reid
Any chance you know about the physics of gluing two pieces of plastic pipe together?
I’m curious about the forces that push the two pieces apart, before the glue sets.
The larger the diameter the greater the force.
terry
Sorry, Terry, I’ve no idea what you’re talking about.
The rate of change of day length would certainly be greater for higher latitudes because you have a greater change of daylength at higher latitudes in the same period of time. As has been said above, the greater slope of the line would indicate the rate of change of daylength.
Another factor involved is the earth’s revolution. The earth is revolving around the sun at the same time it is rotating on it’s axis. This revolution speed increases as the earth approaches perihelion in January in its elliptical orbit abound the sun. This is Keplers Laws. This change in revolution will affect the length of the solar day but not the sidereal day. Still , I don’t think this explains your second graph.
Mr. Reid
I’ve been looking into this phenomenon of joining PVC together.
Did you have any interest in what I’ve come up with?
terry
Not sure what you’re on about, Terry.
Dear Mr: Reid,
I am writing to you , on behalf of our scientific team, in order to kindly ask you whether we are allowed to include the first figure of this webpage, in a scientific report we are planning to publish.
Therefore, we need your written confirmation to do so.
In case you have any questions or you need further clarifications, I remain at your disposal.
Thank you very much in advance for your feedback.
Kind Regards,
Vagia.
Dear Mr. Reid,
I am writing to you, on behalf of the scientific team of Concawe, to kindly ask you whether we are allowed to include the first figure of this webpage in a scientific report we are planning to publish.
In case you have any questions or further clarifications needed, please do not hesitate to contact me.
Kind Regards,
Vagia
Hi Mr. Reid,
I am writing a blog on photoperiod and would like to ask permission to use your graphic on day lengths above. Thank you so much for this super cool website!
Nicky Schauder
Sure, go for it, Nicky.
Thanks, Mr. Reid! It is now up on https://growmyownfood.com/how-to-figure-out-what-to-plant-when/
If two cities are at the same lattitude, Sarmiento, Argentina and Puerto Aisen, Chile, both on the tropic, why would they have different daylengths on Winter solstice. 14.26 and 15.40?
Accidentally closed before completing form
The answer, Suzanne, is that they don’t. On December 22nd the day length in Sarmiento will be 15:38, and on the same day in Puerto Aysén will be 15:36.
Hmm, I thought so. The site I looked at said Sarmiento’s length was 14:26, so that must have been an error. Does surrounding topography in the east/west direction have any impact on sunrise/sunset times?
Sunrise is based on the position of the Sun. Whether or not you can actually *see* the Sun depends on local geography.
For the love of corn biscuits, could someone please explain in layperson’s terms why the hump is so weird-looking in graph 2? Ideally not just mathematically but astronomically. Like, why isn’t the greatest rate of change (of daylight) at the equinoxes?
OH, wait, hang on – is it as a percentage of overall daylight (so, daylight hours is the denominator)? That would make sense. So if we did a different chart, of # minutes lost/gained each day, those would be maximal at the equinoxes right?
Probably!