Imagine you have a cylinder, of any dimensions (i.e. it can be flat like a CD, or tall like a drink can). How fast can you possibly rotate that cylinder?

When an object is spun, the centrifugal forces in its rotating reference frame try to pull it apart. It turns out that the maximum speed that the outside edge of a cylinder can rotate at is given by:

where is the ultimate tensile strength of the material and is the material’s density.

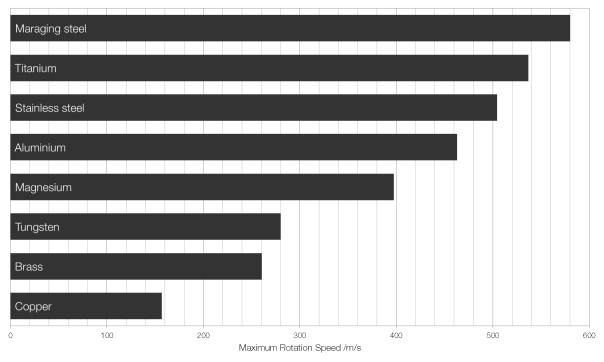
The largest value for metals is that of maraging steels, whose production and distribution is carefully monitored, as it can be used in fast-rotating uranium enrichment centrifuges. (It is also used in the construction of golf clubs and some specialist bicycles.) These centrifuges spin at speeds up to 1500 revolutions per second (90 000 revolutions per minute) and are therefore right on the edge of the capability of the steel to hold itself together.

A cascade of uranium centrifuges.

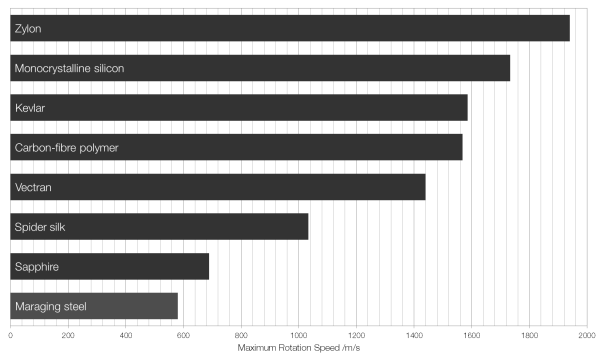
You would be forgiven for thinking that metals would score best in this particular test, but even the strongest metals are easily beaten into submission by crystals and carefully crafted polymers like Vectran™, Kevlar™, and Zylon™.