The numbers drawn in the Israeli national lottery on 16th October were exactly the same as those drawn three weeks previously on 21st September. This has led to a storm of protest, with many suggesting that the lottery is somehow “fixed”.

In the Israeli lottery you pick 6 balls from a possible 37, and 1 from a possible 8. The chances of correctly picking 6 from 37 is 1 in 2324784.* Multiply this by the 1 in 8 chance of picking the second number gives a total probability of winning the jackpot in the Israeli lottery of 1 in 18598272.
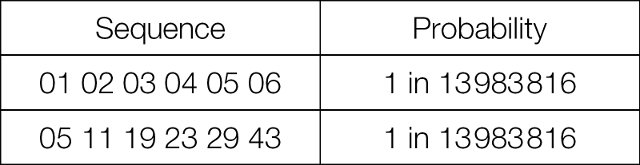
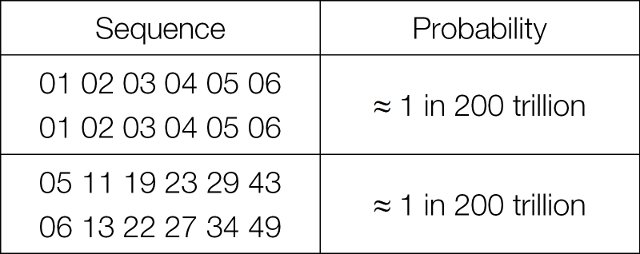
You might think it illogical to play 1, 2, 3, 4, 5, 6 as numbers, on the grounds that a sequential sequence of numbers is less likely to occur than a random sequence such as 5, 11, 19, 23, 29, 43. But this is not true; the probability of any combination of numbers – sequential or otherwise – is the same. The lottery machine does not “know” what numbers have come up previously (or in previous weeks) and cannot set out to “avoid” creating sequential sequences.
 (Selecting 6 balls from 49, as in the UK National Lottery)
(Selecting 6 balls from 49, as in the UK National Lottery)
The chance of the same numbers coming up two weeks in a row are exactly the same as any other combination of numbers.
Human beings are not good at generating random sequences, or at recognising truly random sequences; the tendency of human beings to see significance in randomness is called apophenia. This is what led to the protests in Israel: people saw significance (“cheating”) in the randomly selected lottery numbers.
Apophenia is more commonly associated with visual and audible stimuli, a specific type of apophenia called pareidolia. This tendency to see patterns in randomness is what leads to sightings of a face on Mars or religious figures in toast or wood grain.
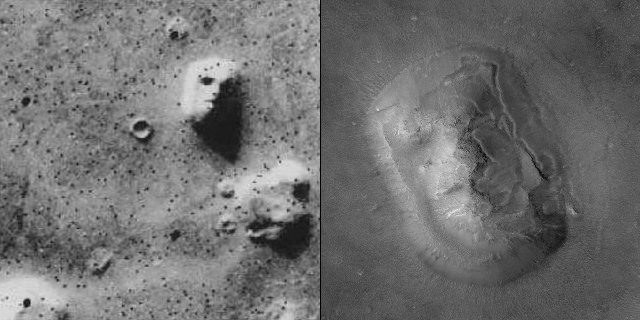
In the image above the original “Face on Mars” image from 1976 is on the left, and a higher-resolution image of the same geological feature from 2001 is on the right.
* You can calculate this yourself using a scientific calculator with an “nCr” (combinations) button: 37C6 is 2324784. This is calculated by doing n!/r!(n-r)!.
Here is a nice Derren Brown episode on a similar theme of superstition (also featuring some national lottery stuff)
http://www.youtube.com/verify_age?next_url=http%3A//www.youtube.com/watch%3Fv%3DjhRyaEypnuE