Analemma

,

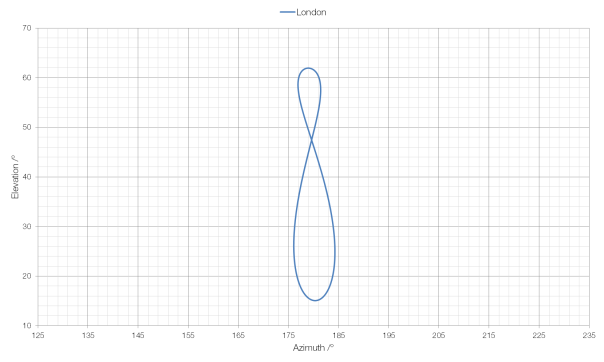
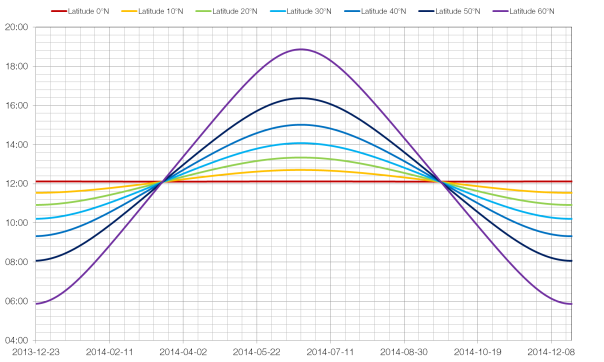
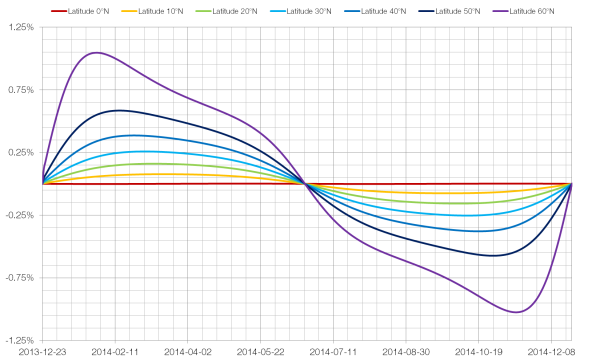
If you took a picture of the Sun every day at noon and then compared the position of the Sun in each of the photographs you’d find that it was in a different place every day. If you joined the positions of the Sun together you’d form an analemma.

analemma-trinity

Source

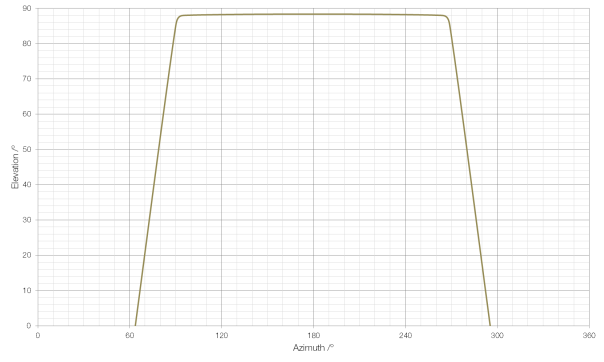
An analemma of the Sun’s position as measured from London is shown above. Elevation, on the y-axis is the angle between the horizon and the Sun, and azimuth, on the x-axis is the compass bearing of the Sun (for example, 90° is due east and 180° is due south).

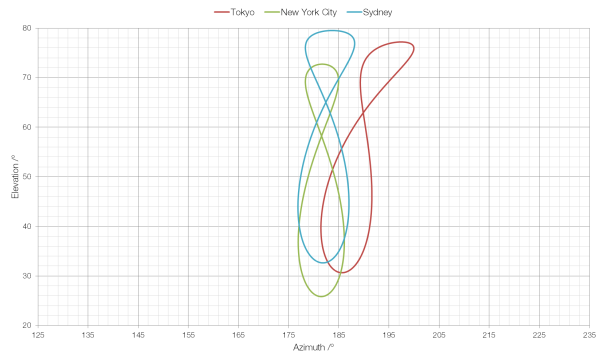
The shape and size of a solar analemma will vary depending on your position on Earth.

analemma-tokyo-newyork-sydney

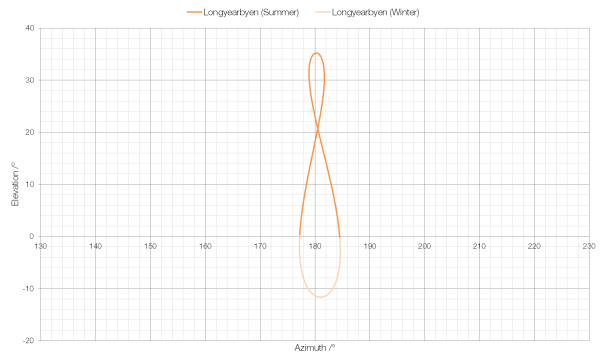
In some cases, such as in Longyearbyen, the world’s northernmost town, the Sun does not rise above the horizon on some days.

analemma-longyearbyen

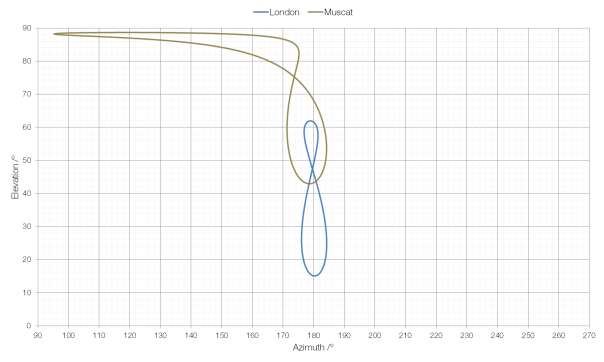
At locations near the Tropics of Cancer and Capricorn, for example Muscat in Oman, the analemma has a very “lopsided” shape.

As you can see, at some points in the year (around the Summer Solstice) the Sun is almost due east, even at noon. This is because the Tropics of Cancer and Capricorn are the northernmost and southernmost points respectively at which the Sun can appear directly overhead, and here the Sun rises around east-northeast and sets around west-northwest, rather than east and west. Suncalc allows you to play with location and the time of year to visualise the position of the Sun during the day.

sunposition-muscat

The position of the Sun during the summer solstice as seen from Muscat.

How Fast Can You Spin?

Imagine you have a cylinder, of any dimensions (i.e. it can be flat like a CD, or tall like a drink can). How fast can you possibly rotate that cylinder?

When an object is spun, the centrifugal forces in its rotating reference frame try to pull it apart. It turns out that the maximum speed that the outside edge of a cylinder can rotate at is given by:

v_{max} = \sqrt{\frac{\sigma}{\rho}}

where \sigma is the ultimate tensile strength of the material and \rho is the material’s density.

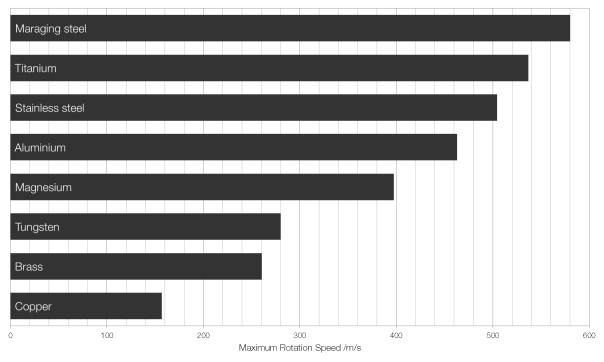
maximum-rotation-speed-metals

The largest value for metals is that of maraging steels, whose production and distribution is carefully monitored, as it can be used in fast-rotating uranium enrichment centrifuges. (It is also used in the construction of golf clubs and some specialist bicycles.) These centrifuges spin at speeds up to 1500 revolutions per second (90 000 revolutions per minute) and are therefore right on the edge of the capability of the steel to hold itself together.

centrifuge-cascade

A cascade of uranium centrifuges.

You would be forgiven for thinking that metals would score best in this particular test, but even the strongest metals are easily beaten into submission by crystals and carefully crafted polymers like Vectran™, Kevlar™, and Zylon™.

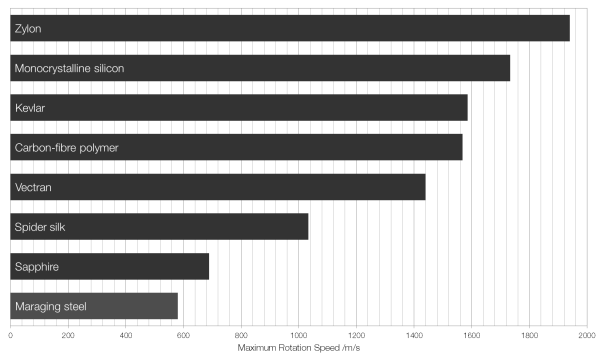
maximum-rotation-speed-other

Change in Day Length with Latitude

,

As the Earth moves around the Sun, the length of the day (defined as the time between sunrise and sunset) changes. The extent to which it changes depends on latitude, as shown in the graph below:

As you can see, the length of a day changes far more during the year at higher latitudes than at lower latitudes. (Latitudes beyond 66°33′ are not shown because the Sun does not always rise or set at these latitudes.) The graph runs from one winter solstice to the next, with the two equinoxes clearly visible in March and September.

It’s quite interesting to look at by how much the length of a day changes every day. This graph would have the same shape as the previous one, but not if we look at percentage change. In a way, this gives an impression of how quickly it appears that “the nights are drawing in”. percentage-change-day-length

At higher latitudes the length of day changes quite noticeably in early January and mid-November.  In some situations two adjacent days are different in length by nearly five minutes, and at some points the day loses nearly fourty minutes over the course of a single week.

Base Bleed Artillery

,

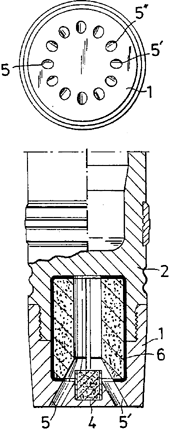base-bleed-patentMost of the drag on an artillery shell comes from friction between the nose of the shell and the air, as the shell pushes air out of the way at very high speeds. But some of the drag on a shell comes from the sucking effect of the vacuum left behind the shell as it pushes air in front out of the way faster than air can move to fill the space left behind.

To combat this, many artillery shells employ a system called base bleed in which the shell produces gas at its rear to fill this vacuum. This gas produces very little thrust, but by reducing the effect of the vacuum it increases the range of the shell enormously, typically by around 30%. On the diagram on the right (taken from this patent) the top image shows a view from below, with the gas generator’s exhaust labelled “5”. The housing of the gas generator is labelled “1” and the casing of the shell “2”. The igniter that starts the gas generator is labelled “4” and the fuel charge that produces the gas is labelled “6”.