Which university course is most popular?

,

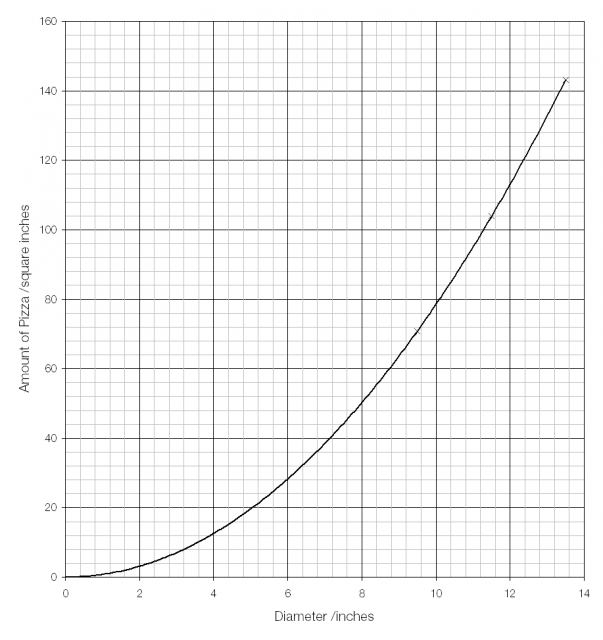
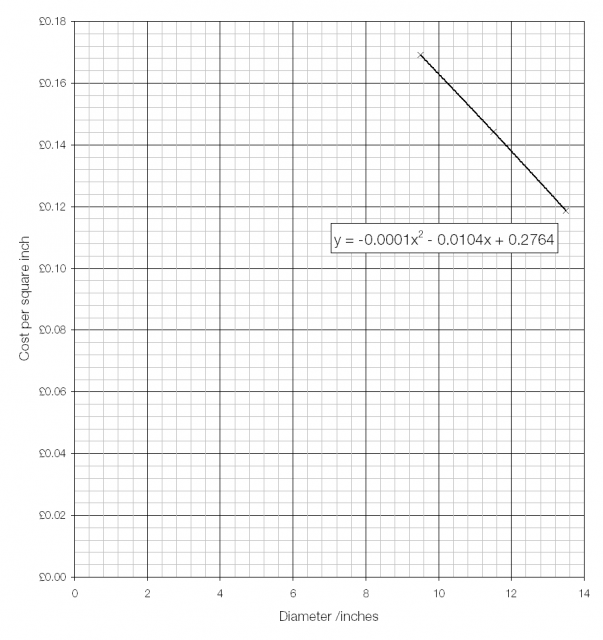
UCAS provides a great deal of statistical information about university applications. One of the most interesting datasets compares the number of applicants for each course with the number of places available.

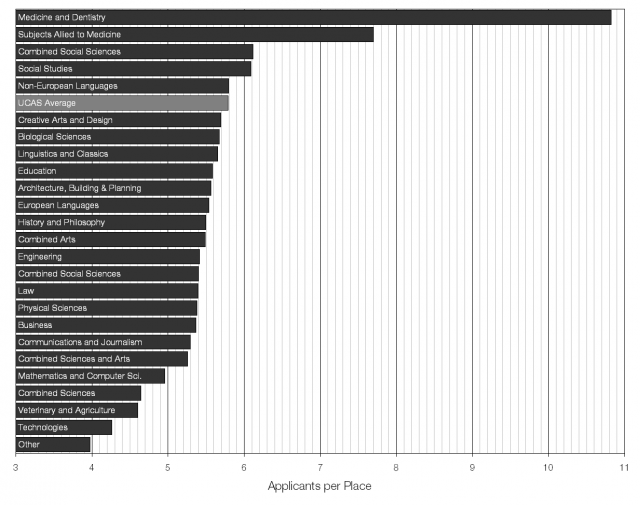(Note that the scale starts at three applicants per place, not at zero.)

Medicine, and subjects related to medicine like anatomy and nursing are the most popular by quite a large margin. The least popular are the technology subjects like metallurgy and materials science.

Ignoring non-specific “any area of study” courses, and those courses with less than a hundred places available, the top ten most popular courses in the country are:

  1. Medicine (A1) – 10.85 applicants per place
  2. Dentistry (A2) – 10.63 applicants per place
  3. Anatomy, Physiology and Pathology (B1) – 9.19
  4. Japanese Studies (T2) – 9.02
  5. Nursing (B7) – 8.89
  6. Veterinary Medicine (D1) – 8.74
  7. Medical Technology (B8) – 8.10
  8. Teacher Training (X1) – 7.90
  9. Aural and Oral Sciences (B6) – 7.58
  10. Microbiology (C5) – 7.56

Within the Physical Sciences astronomy and physics come out top, at 5.88 and 5.86 applicants per place respectively; and of the Biological Sciences microbiology is the most popular (7.56 applicants per place). Of the three “school sciences” physics is the clear winner (5.86) over biology (5.53) and chemistry (5.50).

Understanding the problem with RSA

, ,

Recent reports suggest that the very commonly used RSA encryption algorithm has significant security flaws. I couldn’t find a good explanation of the mathematical problem that causes these flaws online, but I think I’ve worked it out below.

The security of RSA keys rests on the difficulty of factorising the product (usually called n) of two large primes (usually called p and q). Multiplying p and q together is a very quick operation, but working out which p and q were multipled multiplied together to make a given n is very time consuming. If you don’t believe me, see how quickly you can multiply 3259 and 6553; and compare this with the time it takes you to work out which two prime numbers were multiplied together to make 60557843.

In cryptography, n is the public key and is made widely available, whereas p and q make up the private key and must be kept secret. Public keys are usually published to keyservers (here’s mine) and this means that they can be freely downloaded.

Researchers from the Ecole Polytechnique Fédérale de Lausanne in Switzerland downloaded 11.4 million RSA keys and discovered that a number of RSA public keys share a prime factor; that is, they have a different n with one overlapping p or q. This is problematic because finding the greatest common denominator of two numbers is a very quick process when compared with the time taken for prime factorisation.

If we take 60557843 (from above) and compare it with, for example, 15381367 we can very quickly find that they share 7741 as a factor, and with that piece of information we can find the other prime numbers very quickly.

This should not be a problem, because the prime numbers used in encryption are very large (usually hundreds or thousands of digits) and the chance of a “collision” is very small. But if the system used by the computer for generating prime numbers is not truly random then two computers using the same system are likely to produce the same prime numbers and these collisions become far more likely; the researchers found that about 0.38% (1 in 263) of keys were “faulty” in this way.

In conclusion, the problem exists not with the RSA algorithm itself but with the pseudo-random number generators used in RSA systems. Those generating encryption keys should ensure they use a hardware random number generator, one that uses a truly random process such as radioactive decay, to generate their random numbers.

How big are pizzas?

,

Is a 12-inch pizza twice as big as a 6-inch pizza?

Simply put, no. The amount of pizza (its area) is proportional to the square of its diameter, so a 12-inch pizza is actually four times bigger than a 6-inch one.

Looking at the cost per square inch shows an interesting pattern: as size increases, the cost per square inch goes down. (Data from Dominos Pizza.)

If we take the trend that the data is following and solve the equation of the trendline (line of best fit) then we find two possible solutions: the cost per square inch falls to £0.00 at a diameter of either −128 inches or 22 inches. Since a pizza with a diameter of negative 128 inches is clearly ridiculous, it’s the free 22-inch pizza that is interesting.

 

Shapes of equal width

,

Circular objects roll because a circle is a shape of equal width. No matter where you measure from, the distance from one side to the other (through the centre) is the same. But circles aren’t the only shape with this property.

Two British coins are shapes of equal width: the 20p (21.4 mm) and 50p (27.3 mm) coin. Having an equal width makes the coins able to roll and prevents them from getting stuck in machinery. Shapes of equal width also make good manhole covers; because no “side” is any shorter than any other, it is impossible for the cover to fall down the manhole. Circles are easiest to make which is why most manhole covers are circular.