On the chance of dying in a game of Russian roulette

In a standard game of Russian roulette one bullet is inserted into an otherwise empty “six-shooter” revolver and the cylinder is then spun. Each player then takes turns putting the gun to their head and pulling the trigger until one of them dies.

So if you are forced to play a game of Russian roulette, is there any advantage to going first? Or to going last? Or is it best to play somewhere in the middle?

You might think that as the game progresses your chance of dying increases. In the first round there is a 1 in 6 chance of the bullet being lined up with the barrel; in the second round the chance rises to 1 in 5, all the way through to the final sixth round where the chance is 1 in 1, or certain.

But this is not correct, as you haven’t taken into account the chance that you won’t have to play because someone has already shot themselves in the face. If you multiply the chance of a bullet being in the chamber with the chance of having to play you can calculate the risk of dying in each round.

  • 1st round: 1/6 chance of dying × 6/6 chance of having to play = 1 in 6
  • 2nd round: 1/5 chance of dying × 5/6 chance of having to play = 1 in 6
  • 3rd round: 1/4 chance of dying × 4/6 chance of having to play = 1 in 6
  • 4th round: 1/3 chance of dying × 3/6 chance of having to play = 1 in 6
  • 5th round: 1/2 chance of dying × 2/6 chance of having to play = 1 in 6
  • 6th round: 1/1 chance of dying × 1/6 chance of having to play = 1 in 6

So the answer is no, the turn you take in a game of Russian roulette does not make a difference. Suffice it to say that playing a game of Russian roulette in any way is a Really Bad Idea.

Vitamin D is not a vitamin

,

Vitamin D is not a single chemical but rather a group of related compounds: ergocalciferol (vitamin D2), a 1:1 mixture of ergocalciferol and lumisterol (vitamin D1), cholecalciferol (vitamin D3), 22-dihydroergocalciferol (vitamin D4) and sitocalciferol (vitamin D5).

When these compounds reach the liver they are converted to the prohormone calcidiol and then to calcitriol by both the kidneys and by macrophages in the immune system. Calcitriol is a hormone that regulates the concentration of calcium and phosphates in the blood and this is why vitamin D is essential for the growth and remodelling of bone and why a vitamin D deficiency leads to rickets.

A molecule of cholecalciferol.

A vitamin is a substance which the body requires but which it cannot produce by itself. Vitamin D does not fall into this category because the body can produce its own Vitamin D when exposed to sunlight: the major forms of vitamin D, the D2 and D3 forms, are produced in the skin when precursor chemicals (provitamins) react with ultraviolet light.

Vitamin D3 is formed when 7-dehydrocholesterol, itself formed by the oxidation of cholesterol from dietary fats*, reacts with medium wave ultraviolet (UVB) light with wavelengths between 270 and 300 nanometres. Vitamin D2 is formed in a similar reaction when dietary ergosterol reacts with UVB light to form viosterol and then D2. Fungi are particularly high in ergosterol, making them an important source of provitamin D for vegans.

* This is debated, see for example Hartmut Glossmann, “Origin of 7-Dehydrocholesterol (Provitamin D) in the Skin”, Journal of Investigative Dermatology 130 (2010): 2139–2141. doi:10.1038/jid.2010.118.

The plane that shot itself down

The Grumman F-11 Tiger was the US Navy’s first supersonic fighter jet. It came equipped with four Colt Mark-12 cannons that fired 20mm projectiles at more than 1000 metres per second.

Grumman F-11 Tiger, serial number 138620

In September 1956 Thomas W. Attridge, a Grumman test pilot, was flying Tiger #620 in a test flight over the Atlantic Ocean; part of this test flight was to test-fire the Tiger’s cannons. At 20 000 feet Attridge entered a shallow 20° dive and at an altitude of 13 000 feet fired a 70-round burst from one of the cannons. He then activated the Tiger’s afterburners and entered a steeper dive, firing a 55-round burst from the cannon at 7000 feet to empty the cannon’s gun belt.

At this point three of the rounds that he had fired at the higher altitude, which had been slowed by air resistance and which had curved towards the Earth under the effect of gravity, struck the aeroplane’s windshield, nose cone and one of the engine intakes. With reduced engine power available Attridge was unable to return to Grumman’s Long Island airfield and when the engine finally died he was forced to crash land, 800 metres short of the runway.

Despite the unused fuel catching fire, and unfired ammunition from the other cannons “cooking off“, Attridge survived with only a broken leg and three damaged vertebrae; had the cannons been armed with explosive rounds, as would normally be the case, it is unlikely that he would have survived. Attridge later went on to become the project manager for LM-3, the first Apollo Lunar Module to be rated for human spaceflight, which was used as part of the Apollo 9 mission.

In 1973 another Grumman test pilot, Pete Purvis, also shot down his own plane,* this time  with a dummy AIM-7E Sparrow III air-to-air missile that pitched upwards after being released from its hardpoint and struck the wing of the F-14 Tomcat that Purvis was flying. Both Purvis and his Weapons Systems Officer ejected safely.

via Futility Closet

* Source: The Day I Shot Myself Down by Pete Purvis. Purvis also worked on the Fulton Skyhook recovery system.

Orbits

,

Thanks to my Dad for the inspiration for this post.

Earth is orbited by thousands of artificial satellites (and one natural one). These satellites orbit in a number of different ways according to their purpose.

Low Earth Orbit (LEO)

Examples: International Space Station, Hubble Space Telescope, Iridium communication satellites.

Objects in LEO orbit at between 200 and 2000 kilometres from Earth. The low distance from Earth means that it is relatively easy (in terms of energy/fuel) to get into LEO and this orbit is therefore popular. This popularity is boosted by the fact that devices on Earth’s surface do not need to be high-powered to transmit a signal to the satellite. Objects in LEO orbit the Earth about once every 90 minutes and therefore do not remain fixed over a given location for any length of time, requiring that a constellation of satellites be present to provide continuous coverage of/to any one area. For example, the Iridium satellite phone constellation is composed of sixty-six active satellites orbiting at about 780 kilometres above Earth.

Current position of: ISS and Hubble Space Telescope.

Medium Earth Orbit (MEO)

Examples: Global Positioning System (GPS), GLONASS and Galilieo positioning systems.

Satellites in MEO orbit between 2000 and 35 000 kilometres. At this orbit fewer satellites are required to cover the globe: GPS uses thirty-one satellites orbiting at 2o 200 km; and the Russian equivalent, Glonass, uses twenty-four satellites orbiting at 19 100 km. At this distance devices that communicate with satellites have to be high-powered to reach them, but in the case of navigation satellites, which are transmit only,* this is not a problem.

Current position of: GPS Navstar satellites and GLONASS Cosmos satellites.

Geosynchronous Orbit

Examples: Satellite television broadcasting, weather and reconnaissance satellites.

A geosynchronous orbit is one that is in sync with the rotation of Earth: it takes geosynchronous satellites exactly one day to complete one orbit. If a geosynchronous satellite is placed in the same plane as the equator then that satellite is said to be geostationary – relative to an observer on Earth it remains in the same place in the sky all the time. This means that the antennae used to communicate with geostationary satellites can remain in a fixed position – they do not have to move to track the satellite as it moves across the sky.

The idea of a geostationary satellite was popularised by the science fiction author Arthur C. Clarke in an article for Wireless World magazine entitled Extra-Terrestrial Relays – Can Rocket Stations Give World-wide Radio Coverage? so geostationary orbits are sometimes known as Clarke Orbits.

Calculating the height of a geostationary orbit is relatively simple. Any object moving in a circle requires a centripetal force towards the centre of that circle to keep it moving on a curved path. By setting this centripetal force equal to the force of Earth’s gravity pulling on the satellite and solving to find the radius of the circle you find that geostationary satellites orbit at 35 768 kilometres above Earth.†

Not all geosynchronous orbits are geostationary. A geosynchronous polar orbit, in which the satellite passes over both poles causes the satellite to be above the same location at the same time every day, which is useful in making day-to-day comparisons. When using this system more than one satellite is required because each satellite will spend a large amount of time facing the dark (i.e. non sun-facing) side of the Earth.

Polar Orbit

Examples: Imaging/reconnaissance satellites

A polar orbit is one in which a satellite passes over both of Earth’s geographic poles as it orbits; on each orbit it will therefore be above a strip of land west (as the earth rotates east-to-west) of the piece it previously orbited. Polar orbits like this are useful because a low number of satellites can image the entire Earth. NASA’s MODIS system is composed of two satellites (Terra and Aqua) that image the entire Earth once every one or two days.

An image showing one day of swaths from the TRMM satellite.

Current position of: Terra, Aqua and TRMM satellites.

Elliptical Orbits

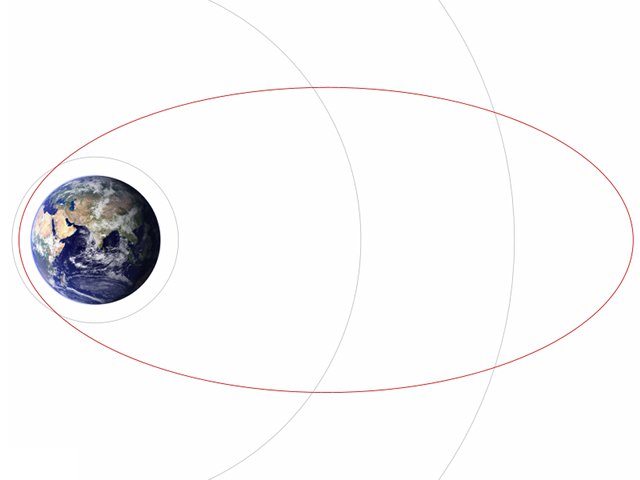
Examples: Specialised communication satellites, Sirius satellite radio

All of the previous orbits are circular, each satellite remains at a constant distance from Earth’s surface. Satellites in elliptical orbits change their distance from Earth, speeding up as they approach closer to Earth and slowing down as they move away. Satellites in elliptical orbits spend long periods of time over one area of Earth, providing coverage of that particular area with a small number of satellites.

A communication satellite in a geostationary orbit is further away from northern latitudes than the equator and therefore requires more power to be able to reach these locations. Russian Molniya communication satellites (after which the Molniya orbit is named) orbit at an angle of 63° to the equator at a distance between 500 and 40 000 km and take half a day to complete one orbit, enabling them to loiter above 55°N for six hours a day, which means that only three satellites are required for all-day coverage at high latitudes (as they can broadcast to 55°N from below this latitude). The Sirius Satellite Radio system, which broadcasts to North America, uses three satellites in Tundra orbits which are similar to Molniya orbits in their inclination and eccentricity, but with an orbital period of one day, making them geosynchronous. In contrast, the XM satellite radio system uses two satellites placed in geostationary orbits at longitudes of 85°W and 115°W (corresponding approximately to the west and east coasts of the USA).

Graveyard Orbit

Graveyard orbits are where satellites go to die. At the end of their useful life, if there isn’t enough energy to push a satellite into Earth’s atmosphere where it will burn up (or land in the “spacecraft cemetery” in the Southern Pacific Ocean off the coast of New Zealand) then satellites are pushed into an orbit above their normal location so that they do not collide with active satellites in their original orbit.

An image of space debris from the European Space Agency.

You can use WolframAlpha to find out which satellites are currently above your location.

* The US Department of Defense, which runs the GPS, does transmit updates to the satellites, from the Master Control Station at Schriever Air Force Base and from one of four monitoring stations on the islands of Hawaii and Kwajalein in the Pacific Ocean, the Ascension Islands in the South Atlantic Ocean and Diego Garcia in the central Indian Ocean.

† For the interested, the radius of a geostationary orbit from the centre of a planet with mass M that rotates once every T seconds is the third root of GMT2/4π2 where G is the universal constant of gravitation.