
When the topic of climate change comes up, a common refrain is that the melting of icebergs is going to drown us all. This is not true. Even if every iceberg in the world melted, we wouldn’t notice the difference.
Archimedes’ Principle states that an object which displaces a fluid (i.e. a liquid or a gas) will experience an upward force that is equal to the weight of the fluid displaced. If an object displaces one cubic metre of water it will experience an upward force of around 9810 newtons, regardless of what it is made from. If its own weight is greater than 9810?N it will sink; if it is less than this it will float.
The density of ice is approximately 920 kilograms per cubic metre, and the density of seawater is approximately 1025?kg/m3. If a cube of ice with sides of one metre is placed into water it will push down on the water with a force of 9030?N (920?kg × 9.81?N/kg), and the water will push upwards on the ice with a force of 10?100?N (1025?kg × 9.81?N/kg). There will therefore be a net upward force on the ice cube of 1030?N and it will float to the surface. However, the ice cube will not float completely above the surface of the water – some of the ice cube will stay submerged.
The volume of the ice cube that is submerged will be equal to the volume of water that has the same weight as the cube itself, or mathematically:
We can find the volume of the ice that is submerged by calculating:

That is, the volume of the ice that is submerged ( ) multiplied by the density of the water (
) multiplied by the density of the water (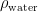 ) multiplied by the strength of the gravitational field (
) multiplied by the strength of the gravitational field (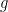 ) is equal to the weight of the ice cube (
) is equal to the weight of the ice cube (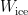 ).
).

An iceberg, with the submerged portion clearly visible underwater.
Using the data we know, we find that the volume of ice submerged is 0.898?m3. This result applies regardless of the shape or size of our ice cube, so we know that 89.9% of any iceberg is below the surface of the water, and 10.2% is above. People seem to be worried that when the ice melts, this above-surface water will be added to the volume of the world’s oceans. However, this fails to take into account the different densities of ice and liquid water. As the ice melts into liquid water its density increases and thus the level of the water remains the same. You can prove this to yourself very easily: place an ice cube into a glass of water, draw a line at the level of the water, and wait for the ice to melt. The level of the water will not climb above your original line.*
What people should be worried about is not icebergs but ice caps. Ice caps are ice that it sitting on land and therefore is not already displacing water. If this ice melts and runs into the oceans it certainly will increase sea levels.
What people should also be worried about is that the density of water changes with temperature. As climate change increases the temperature of the oceans it will expand, and again sea levels will rise.
Note: This is all based on a mathematical-physical model. When other factors are taken into consideration, melting icebergs may contribute very slightly (about 50 micrometres per year) to an increase in sea level.



 Old style figures
Old style figures Lining figures
Lining figures


