The Kármán Line, at 100 kilometres above sea level, is commonly taken to be the boundary between Earth’s atmosphere and space. But why?
An aircraft generates lift by moving through air.
where 
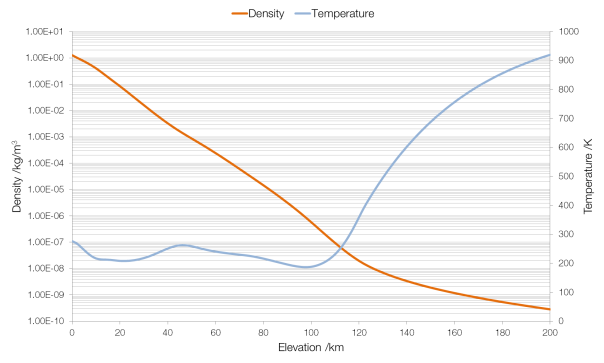
Data from NASA MSIS E-90 atmosphere model. Note that density is plotted on a logarithmic scale and (absolute) temperature on a linear scale.
The density of air changes with elevation (altitude is height above ground, elevation is height above sea level). Therefore, keeping all other factors the same (which would be the case for an aircraft, which cannot change the area of its wings or its lift coefficient), as the air becomes less dense an aircraft must increase its speed to stay airborne. A Boeing 747-400 has a wing area (planform) of 541.2 square metres and a lift coefficient of around 0.5. Assuming that it flies empty, with a mass of 178?800 kilograms (weight 1?754?000 N), the speed it will need to fly to generate the required lift changes rapidly as the air becomes thinner. (At an elevation of 200?km a 747-400 would have to fly at nearly twenty thousand times the speed of sound.)
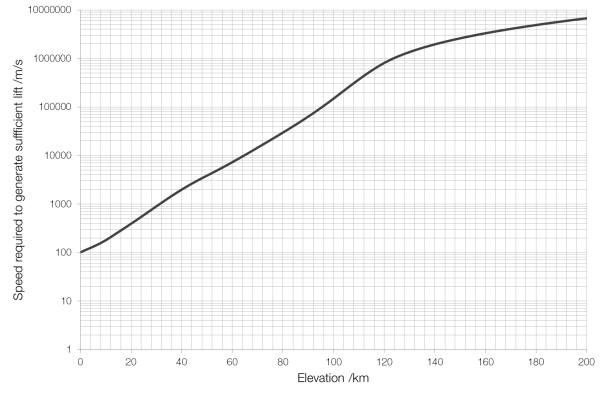
Speed required at elevation for a Boeing 747-400.
The cruising speed of a 747-400 is about Mach 0.85 or 290 metres per second, which limits the 747-400 to an elevation of around 16 km. (In reality it flies much lower, around 12?km, for safety and fuel consumption reasons.) The record elevation for sustained horizontal flight by a ground-launched aircraft is 36?240 m by a MiG-25M, which was, at the time, one of the fastest military aircraft with a top speed of Mach 2.83.
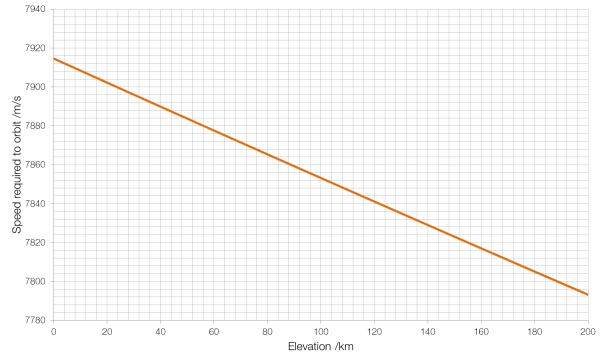
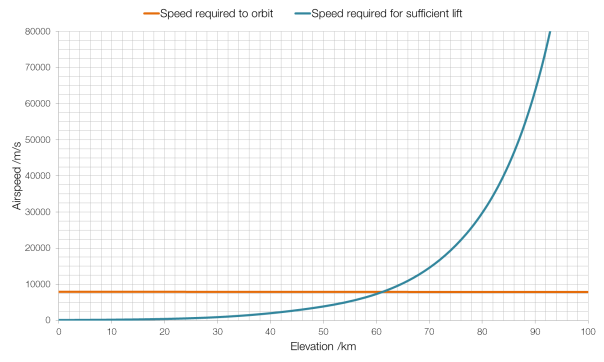
The Kármán Line, at an elevation of 100?km, is the point at which the atmosphere is so thin (more than a million times thinner than air at sea level) that an aircraft would have to be moving at a speed faster than it could orbit in order to stay in the air. Thus, it is the greatest altitude at which an aircraft could fly in a straight line rather than following the curvature of the Earth.
As you can see from the graph above, for our Boeing 747-400, the Kármán Line is around 61?km, rather than the full one hundred kilometres, because the 747-400 is not the most aerodynamic of aircraft, designed for bulk passenger carrying and cost-efficiency rather than performance.
Thanks for sharing informative content with detailed images and graphlines. Keep us updated more with amazing article like this.
how is a planes flight horizontal over the earths surface?
The Earth’s surface is curved.