Monthly Archives: August 2012

Coloured blood

,

One of the main purposes of blood is the transport of oxygen around the body; this oxygen is required for cellular respiration and without it cells in the body will die.

In humans and other vertebrates, oxygen is transported in the blood by a protein called haemoglobin that is contained within red blood cells. Each haemoglobin molecule contains four iron ions to which an oxygen molecule can bind. The oxyhaemoglobin that is formed when oxygen molecules bind to haemoglobin is bright red, which gives blood its red colour.

A haemoglobin molecule. The oxygen binding sites are at the centre of the green haem groups.

It is possible for humans to develop blood with a greenish hue if suffering from a condition called sulphaemoglobinaemia, in which a sulphur atom is incorporated into the haemoglobin molecule.

But haemoglobin is not the only molecule capable of transporting oxygen in blood. In molluscs like crabs, octopuses, oysters, slugs, snails, squid, worms and many others, oxygen is transported by haemocyanin, which contains copper rather than iron.

A haemocyanin molecule. The oxygen binding site is at the centre, in between the two copper atoms.

Deoxygenated haemocyanin is grey or pale yellow, and when oxygenated (for example by exposure to air) the oxyhaemocyanin is a dark blue colour.

The interior of a crab shell. The purple colouring is due to the presence of oxyhaemocyanin.

There are a number of other oxygen-binding proteins found in nature which give rise to a number of different blood colours. For example, haemerythrin gives some annelids and marine invertebrates pink/violet or clear blood; annelids also use chlorocruorin which gives them red or green blood.

You can see more than half of a neutron star

,

Common sense dictates that if you look at a spherical object like a ball or a planet you can only see half the surface area of that object. But this is not true for neutron stars.

A neutron star is formed when the core of a relatively large star collapses in on itself in a supernova. Neutron stars are incredibly dense: one teaspoon of neutron star can have a mass of more than five trillion kilograms.

One of the best elaborations of Einstein’s Theory of General Relativity was given by John Wheeler:

“Mass tells space-time how to curve, and space-time tells mass how to move.”

But if space-time is curved then anything passing through space, whether it is matter or light, will follow a curved path. The gravitational field of a neutron star is so strong that it warps space, and warps space to such an extent that light emitted behind the star is warped around.

Diagram of a neutron star, viewed face-on.

In the diagram above each chequered section is 30° × 30°; note that both poles of the neutron star are clearly visible. The highlighted section on the right-hand diagram shows the area that would normally be visible if gravitational distortion were not present.

Normally 180° of latitude and longitude would be visible, but in this case the figure is nearly 260°, meaning that more than 70% of the neutron star’s surface area is visible.

Separative Work Units

,

Seperative Work Units (SWUs) are a measurement of the effort required to seperate isotopes of uranium for use in nuclear power stations or nuclear weapons.

The maths behind the calculation of SWUs is quite complicated (Kirk Sorenson has written a great article about calculating SWUs) but what is interesting is to compare the effort required in various situations.

Examples

Little Boy, the sixteen kiloton nuclear weapon that was dropped on Hiroshima during World War II contained fifty kilograms of uranium enriched to 88% and a further fourteen kilograms enriched to 50%. This would require 10800 SWUs (9350 + 1450).

Aside from its work enriching uranium to 5% for use in the Bushehr nuclear power station, Iran has also enriched 98 kg of uranium to 20% [source], requiring 3740 SWUs. To further enrich this fuel, to produce 20 kg of highly enriched uranium – enough for a nuclear weapon – would require a further 370 SWUs.

Data about nuclear-powered submarines is hard to come by, but unclassified sources state that Ohio Class SSBNs of the US Navy are powered by General Electric S8G nuclear reactors using fuel that has been enriched to 97.3%, probably with an initial fuel load of around 400 kg. To produce 400 kg of fuel enriched to 97.3% would require 83700 SWUs.

Sizewell B is the UK’s newest nuclear power station and produces about two gigawatts of electricity (about seventeen billion kWh per year). It uses about thirty tonnes of uranium enriched to about 3.5% per year, which would require 129000 SWUs.

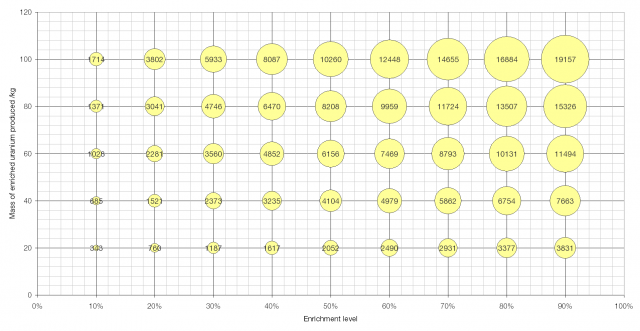
A graph showing the effort required to produce a given amount of enriched uranium to a given level. The area of the bubbles is proportional to the number of SWUs required. Click to enlarge.

It’s worth looking in these cases at the amount of initial uranium required. The greater the desired enrichment level, the greater the initial feed required to yield a given mass of enriched uranium is. In the case of Little Boy, to produce 64 kg of uranium enriched to around 80% would have required more than 12 tonnes (12 096 kg) of initial uranium (and a much larger amount of uranium ore, depending on the grade of ore*). This would result in 12 032 kg of waste depleted uranium, good only for use as ballast, shielding or armor-piercing projectiles. The amount of effort required (the number of SWUs) to enrich this depleted uranium to a usable level would be far too great for proliferation to be a problem.

By far the predominant current method of isotope separation is the use of gas centrifuges, at a cost of around $100 per SWU†; thus the cost of the enrichment required to run Sizewell B for a year would be about $13 million. A newer method, laser enrichment, promises to cut this cost to around $30/SWU, which would bring down the cost of running Sizewell B to only $3.9 million. Unfortunately this would also make enrichment for more nefarious uses cheaper.

SWU calculations depend on the amount of uranium left behind in the “tailings” of the enrichment process. For the purposes of all the figures above this is assumed to be 0.3%. If uranium were to become scarce then this percentage would obviously decrease.

* The highest grade ore in the world comes from the Athabasca Basin in Canda, with a grade of 18%. To yield one kilogram of uranium from Athabasca would require 5.56 kilograms of ore.

† The figures for cost per SWU come from Sharon Weinberger, “Laser plant offers cheap way to make nuclear fuel”, Nature 487: 16-17. DOI: 10.1038/487016a.

Computer designed camouflage

,

In 1996 Canada became the first country to adopt battledress with a camouflage pattern generated by a computer, also known as digital camouflage.

L-R: Simulated CADPAT (Canadian Disruptive Pattern) for temperate, arid and arctic regions.

It is not the pixellated appearance of the pattern from which digital camouflage gets its name. There are a number of pixellated patterns that are not digital camouflage (e.g. Soviet “Birch Leaf”), and a number of digital camouflage patterns that are not pixellated (e.g. Italian “Vegetato”).

Rather the term “digital camouflage” comes from the computer-aided process by which the pattern is developed, using computer models of how human vision works and applying complicated computer techniques such as fractal generation and recursive algorithms employing both macro- and micro-patterns. The hope is that this more scientific approach will result in camouflage patterns with lower detectability, and this seems borne out by the fact that most militaries are now adapting digital camouflage patterns.

Salt flats and giant space mirrors

, ,

A salt flat is formed when a pool of salt water evaporates, depositing salt as it does. This layer of salt builds up over time and seasonal flooding causes a very flat surface to form.

Salar de Uyuni in Bolivia, the largest salt flat in the world.

When covered in water, salt flats become the largest mirrors in the world.

Salt flats are commonly used to calibrate observation satellites, as they provide very large and flat areas (Salar de Uyuni has an area of more than 10 000 square kilometres and varies in height by less than one metre). The surface of salt flats are highly reflective and because they occur in desert areas there is usually very little cloud cover and very clear air.