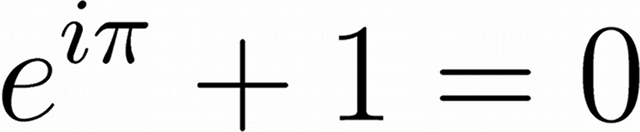
Euler’s Identity, shown above, is often said to be the most beautiful equation in all of science and mathematics.

It links the three basic arithmetic operations:

• Addition, in the +1 term.
• Multiplication, in the iπ term.
• Exponentiation, in the e^iπ term.

It also links five of the most important mathematical constants:

• e, the base of the natural logarithms.
• i, the imaginary number (√−1) on which complex numbers are based.
• π, the ratio of a circle’s circumference to its diameter.
• 1, the multiplicative identity, the basic unit of counting.
• 0, the additive identity that leaves a number unchanged.

Understanding how e^iπ + 1 can equal zero is more difficult.

To begin to understand how to evaluate Euler’s Identity we must first understand about series expansions. The series expansion of a function can be used to calculate the value of this function to an arbitrary degree of precision.

The series expansion of e^x is given by:

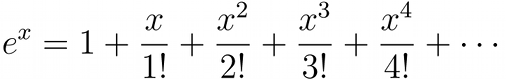
If only the first term is used then e = 1.00, if two terms are used e = 2.00, if three terms are used e = 2.50, if four terms are used e = 2.66, and so on, until an infinite number of terms are used and the exact value of e is given. After only ten terms the value found for e is accurate to better than one part in a million.

The series expansion of e^iπ is therefore given by:

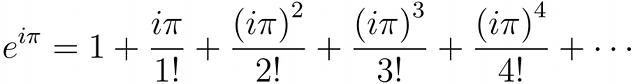
The even powered terms (e.g. i²π², i⁴π⁴) become negative because i²=−1 and the odd powered terms (e.g. i³π³, i⁵π⁵) gain a negative multiple of i.

There are two other important expansions, the expansion of sin(x) and cos(x), two basic trigonometric functions.

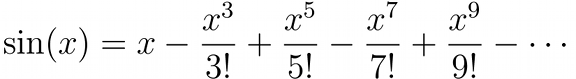
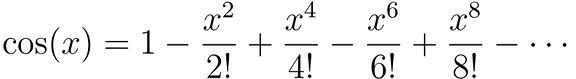
If we collect the terms in the expansions of sin(x) and cos(x) and compare them with the expansion of e^ix we find that:

Inserting π in place of x in that expression yields:

Because cos(π) = −1 and sin(π) = 0 we find that indeed, e^iπ = −1 and therefore e^iπ + 1 = 0.