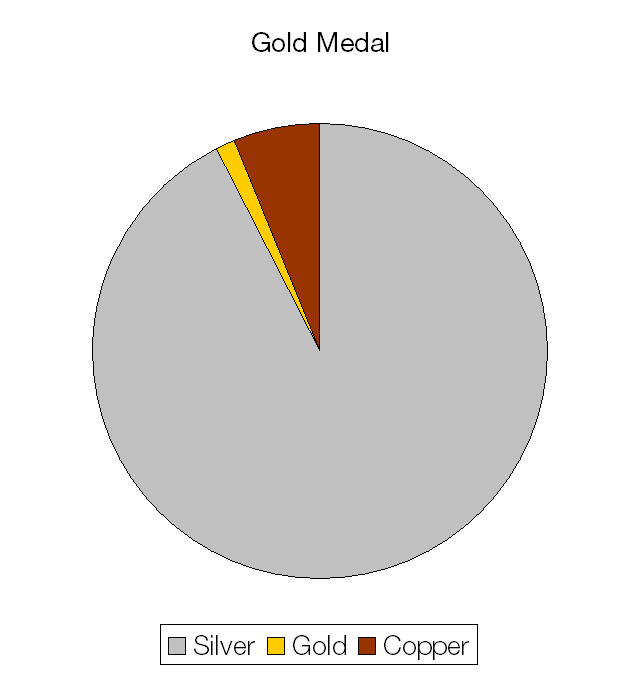
The materials cost of a gold medal is £396.66.
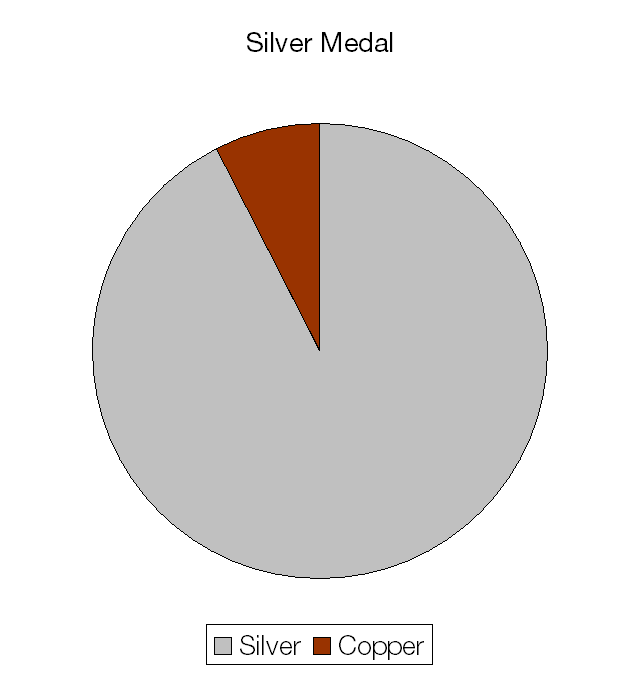
The materials cost of a silver medal is £214.02.
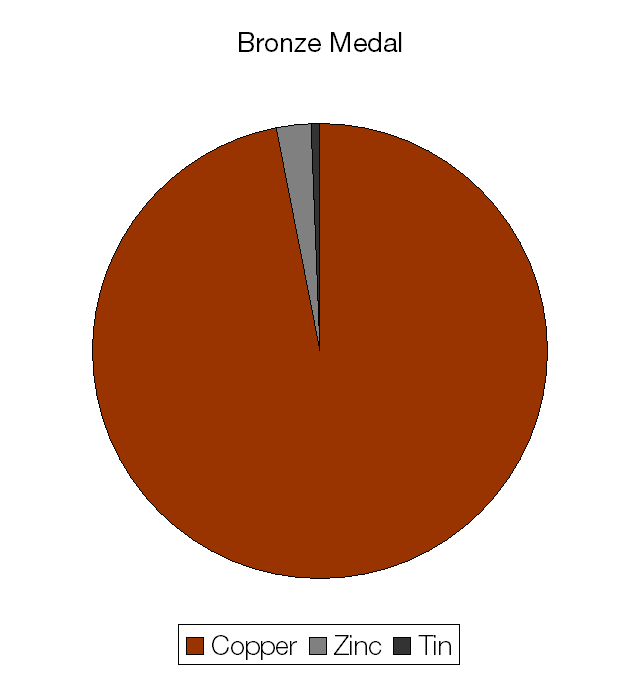
The materials cost of a bronze medal is a measly £1.63.
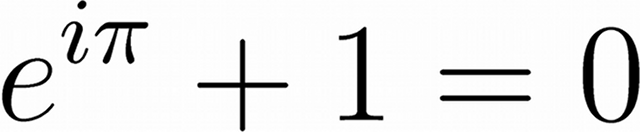
Euler’s Identity, shown above, is often said to be the most beautiful equation in all of science and mathematics.
It links the three basic arithmetic operations:
It also links five of the most important mathematical constants:
Understanding how eiπ + 1 can equal zero is more difficult.
To begin to understand how to evaluate Euler’s Identity we must first understand about series expansions. The series expansion of a function can be used to calculate the value of this function to an arbitrary degree of precision.
The series expansion of ex is given by:
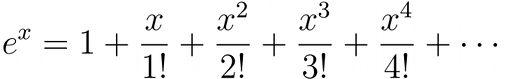
If only the first term is used then e = 1.00, if two terms are used e = 2.00, if three terms are used e = 2.50, if four terms are used e = 2.66, and so on, until an infinite number of terms are used and the exact value of e is given. After only ten terms the value found for e is accurate to better than one part in a million.
The series expansion of eiπ is therefore given by:
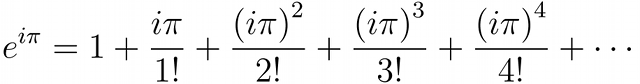
The even powered terms (e.g. i2π2, i4π4) become negative because i2=−1 and the odd powered terms (e.g. i3π3, i5π5) gain a negative multiple of i.
There are two other important expansions, the expansion of sin(x) and cos(x), two basic trigonometric functions.
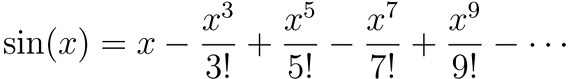
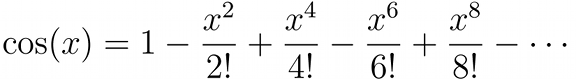
If we collect the terms in the expansions of sin(x) and cos(x) and compare them with the expansion of eix we find that:
![]()
Inserting π in place of x in that expression yields:
![]()
Because cos(π) = −1 and sin(π) = 0 we find that indeed, eiπ = −1 and therefore eiπ + 1 = 0.
In maritime terms there is a difference between a collision and an allision.
When two moving objects strike each other, that is a collision.
When a moving object strikes a stationary object, that is an allision.
The Travelling Salesman Problem is a classic problem in mathematics. The objective of the problem is to find the shortest possible route between a number of cities that visits each city only once and returns to the starting point.
Below is a rendering of the text “MrReid.org” created by solving the Travelling Salesman Problem. If you look carefully you can see that in each case the text is composed of one single line, drawn “without lifting the pen from the page”.
Top to bottom: “MrReid.org” rendered using 1000, 2000, and 5000 nodes. Click to enlarge.
By taking a greyscale image, and turning it into a weighted Voronoi diagram (using Adrian Secord’s algorithm) it is possible to create a “map” in which the “cities” are placed closer together in dark areas and further apart in light ones.


Top: the original panda image. Bottom: weighted Voronoi diagram of panda image (10000 nodes).
By solving the Travelling Salesman Problem for this “map” (using the Nearest Neighbour algorithm for the first pass and and the 2-opt algorithm for subsequent optimisation) the following “route” is produced.

There isn’t really enough contrast between the background and foreground in the original panda image, but it works if you squint a little bit.

Is the Drinking Bird a perpetual motion machine?
Depending on what type of perpetual motion machine is being described, all perpetual motion machines violate either the First or Second Law of Thermodynamics, so the answer is no, the Drinking Bird is not a perpetual motion machine.
So what powers the Drinking Bird? If it is moving it must have kinetic energy and the Principle of the Conservation of Energy says that this kinetic energy must have come from somewhere. It does not come from the water as, despite what you might have read about “water powered cars”*, water is not a fuel and does not store or transfer energy.
The correct answer is that the Drinking Bird is powered by the ambient heat of the room it is placed in. The process that occurs is as follows:
The Drinking Bird is a heat engine that uses the difference in temperature between the head and the base of bird to perform work, transferring thermal energy to kinetic energy. This temperature difference is created by evaporation that is powered by a room’s ambient heat. If you were able to perfectly insulate a room so that no thermal energy could enter or leave then you could cool the room down by leaving a drinking bird running.†
* “Water powered cars” are actually being powered by hydrogen fuel cells. The hydrogen comes from the water and is extracted using electricity, making “water powered cars” actually powered (indirectly) by electricity.
† Friction between the air and the bird, and between the bird and its bearings would transfer some of the bird’s kinetic energy into thermal energy, heating the room back up.