Monthly Archives: June 2012

A-series paper

,

There are not many things in this world that I hate more than Letter Size paper.

Just look at it. Isn’t it horrible? Sitting there being based on outdated imperial units, looking all wonky and fat.

But instead of explaining in great detail why I hate Letter Size paper I’m going to explain why I love its main competitor: A4 size paper.

A4 is the fourth size in the metric International Standard (ISO 216) A-series of paper which runs from A0 (the largest) to A10 (the smallest). The A-series is constructed so that the longer side is 1.414 (√2) times the length of the shorter side, which makes each size in the series composed of two copies of the next-smallest size.

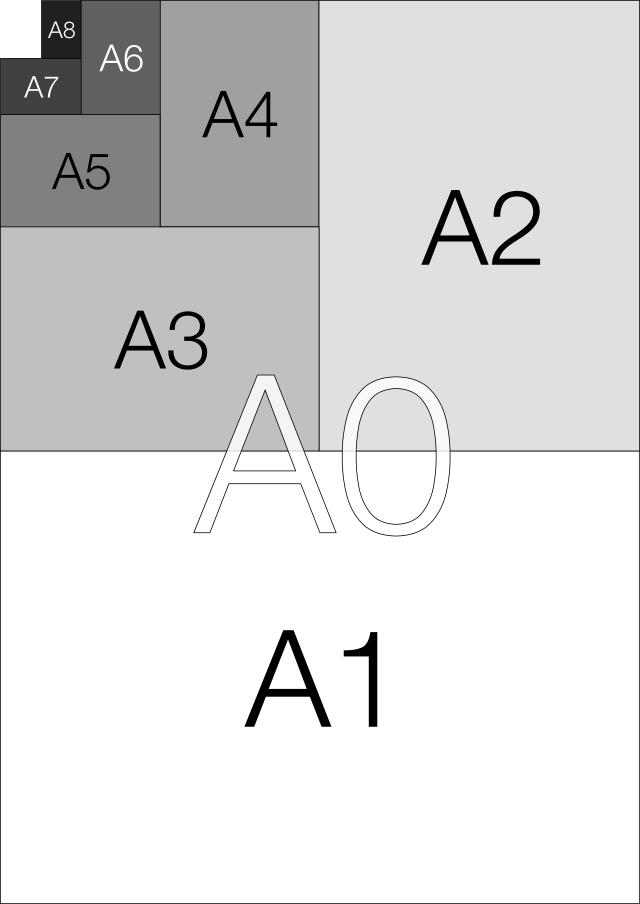
If x is the length of the shortest side then the area of an A-series sheet of paper is 1.414x2. Given that the first size in the series, A0, has an area of 1m2, that means that the short side of Ao is 841 millimetres and the long side 1189 mm. From this, the dimensions of all the remaining sizes in the series can be found.

On the chance of dying in a game of Russian roulette

In a standard game of Russian roulette one bullet is inserted into an otherwise empty “six-shooter” revolver and the cylinder is then spun. Each player then takes turns putting the gun to their head and pulling the trigger until one of them dies.

So if you are forced to play a game of Russian roulette, is there any advantage to going first? Or to going last? Or is it best to play somewhere in the middle?

You might think that as the game progresses your chance of dying increases. In the first round there is a 1 in 6 chance of the bullet being lined up with the barrel; in the second round the chance rises to 1 in 5, all the way through to the final sixth round where the chance is 1 in 1, or certain.

But this is not correct, as you haven’t taken into account the chance that you won’t have to play because someone has already shot themselves in the face. If you multiply the chance of a bullet being in the chamber with the chance of having to play you can calculate the risk of dying in each round.

  • 1st round: 1/6 chance of dying × 6/6 chance of having to play = 1 in 6
  • 2nd round: 1/5 chance of dying × 5/6 chance of having to play = 1 in 6
  • 3rd round: 1/4 chance of dying × 4/6 chance of having to play = 1 in 6
  • 4th round: 1/3 chance of dying × 3/6 chance of having to play = 1 in 6
  • 5th round: 1/2 chance of dying × 2/6 chance of having to play = 1 in 6
  • 6th round: 1/1 chance of dying × 1/6 chance of having to play = 1 in 6

So the answer is no, the turn you take in a game of Russian roulette does not make a difference. Suffice it to say that playing a game of Russian roulette in any way is a Really Bad Idea.