Tag Archives: graph

How to make nicer graphs in Microsoft Excel

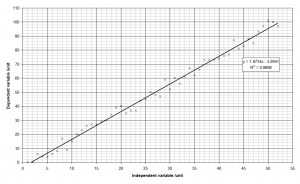
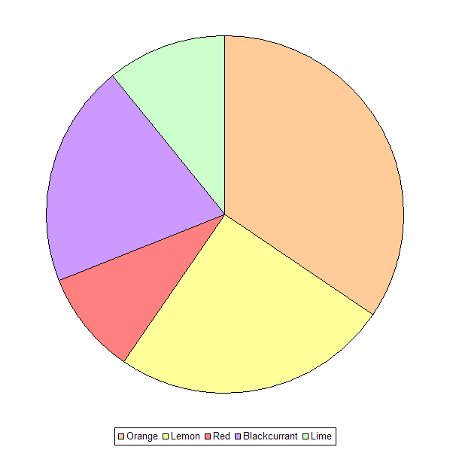
I really hate it when I’m presented with a graph like this one:

Ugly default graph

It’s instantly recognisable as one created in Microsoft Excel. For some reason the default settings in Excel produce some of the the ugliest graphs I’ve ever seen.

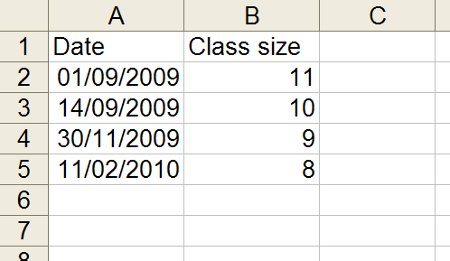
Step 1 – Fix the data points themselves

Nobody in their right mind plots data points as little diamonds – we use crosses. Selecting “Format Data Series” enables you to set the background colour to Transparent and the style to a little cross. The colour of the cross is up to you; I tend to stick with traditional black.

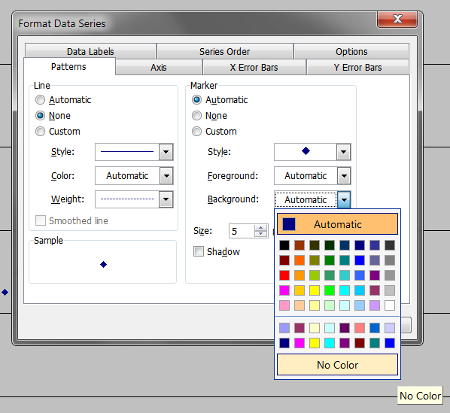
Step 2 – Get rid of the background

Grey background? Why, Excel, why? Set the ‘Plot Area’ colour to none.

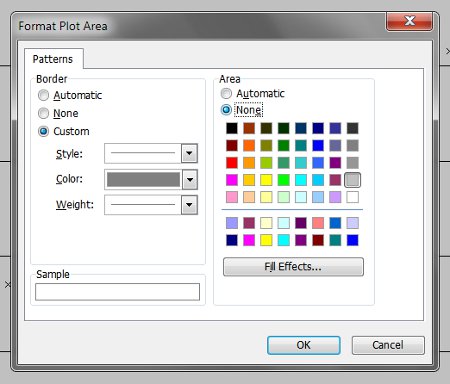
Step  3 – Gridlines

“Standard” graph paper tends to have two sets of lines – thicker major gridlines and thinner minor gridlines. I see no reason why Excel graphs should be any different. Under “Chart Options” there are checkboxes for major/minor gridlines on both the x- and y-axes.

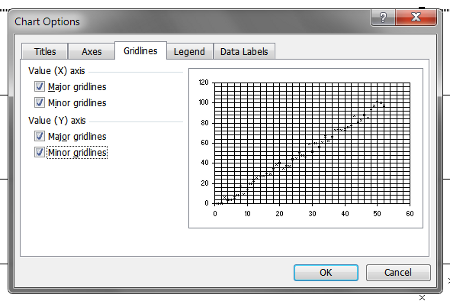
I find that setting the minor gridlines on both axes to a pale grey makes things look nicer. If you’re going to print your graph (or photocopy it) then you’ll want to increase the thickness of the lines too.

Step 4 – The legend

Why Excel puts the legend on the right of the graph I don’t know. Most of the time it’s not needed, and when it is needed it’s far more space-efficient to put it at the top or bottom of the plot area.

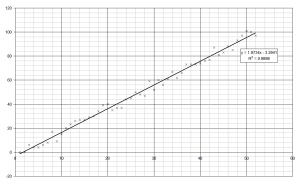
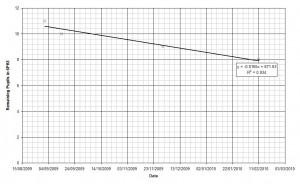
Step 5 – Line of best fit

Excel calls lines of best fit ‘Trendlines’ so make sure you add a trendline. Make sure that you choose the right type – exponential for radioactive decay, power for simple pendula, etc.

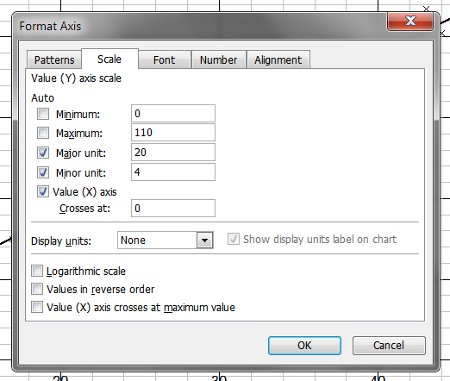
Step 6 – Axes

Your axes need to be properly labelled.

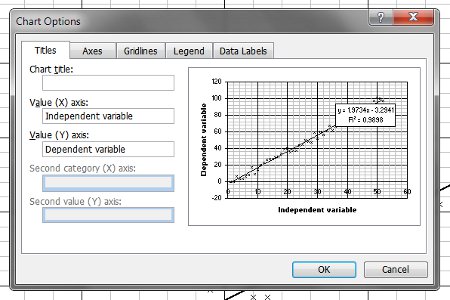
It’s a good idea to adjust the scales as well.

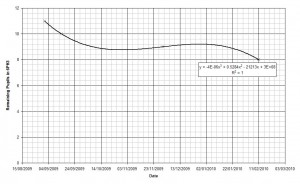
The Finished Product

The dangers of extrapolation

,

Physics isn’t for everyone; every year there’s a pretty good chance that at least one person will drop out of a group (sometimes you get drop ins too). This year one group in particular has lost more pupils than average so I decided to start collecting data.

I plotted the data and added a line of best fit.

The R2 value is 0.934 so there’s fairly good correlation in the dataset. Now that I have an equation linking the date (x) and the number of pupils in the class (y) I can work out when the next pupil will leave the group by setting y to equal seven.

y = −0.0165x + 671.63
7 = −0.0165x + 671.63
x = 40280.61

Excel handles dates in a strange way, so the figure of 40280.61 needs to be converted into a regular date: now I know that the next pupil will leave 6PH3 on the 12th April 2010 (at half past two).

I can even find out when the class will be empty by solving for y=0.

0 = −0.0165x + 671.63
x = 40704.84

The class will finally empty out at 10th June 2011 at twenty past eight.

I thought that perhaps the linear fit wasn’t the best approach so I tried a polynomial fit, which turned out to have an R2 value of exactly 1.

It turns out that this line only has one real solution, and according to that, I won’t run out of pupils until 27th June 2103.

Fruit Gums and graphs

,

All the data from my Fruit Gums experiment has one continuous variable (the number of gums) and one discrete variable variable (either box number or flavour) so the physicist’s standard graph – the x-y scatter plot – isn’t suitable. This made it a good opportunity to try out some different graph/chart types.

A pie chart shows the relative contribution of each item to the whole.

The doughnut chart builds on the pie chart by enabling more than one set of data to be plotted – in this case all three boxes at once.

Bar charts come in two forms: horizontal and vertical. In this case there are two ways to group the bars: by flavour or by box number.

With lots of data a bar chart can become crowded and confusing and that’s where stacked bar charts become useful. A stacked bar chart overcomes this problem and can be done in two different ways: using absolute values or by percentage.