Smiths

,

Most people are familiar with the term “blacksmith” and think that it refers to someone who works with metal, but this isn’t entirely correct. The term “blacksmith” only refers to someone who works with the “black” metals such as iron and steel.

Redsmiths* work with copper, whitesmiths work with light-coloured metals such as pewter or tin and brightsmiths work with silver. Many smiths are known by the type of object they produce, for example a gunsmith makes guns and and a bladesmith makes knives and swords; others are known by the metal they work with: goldsmiths and zincsmiths work with gold and zinc respectively.

* Redsmiths are also known as brownsmiths.

Water in Bermuda

,

Fresh water is very hard to come by on the Islands of Bermuda. There are no lakes, and only a small number of water-collecting “lenses” underground. Rainwater is not salty, as the salt from seawater does not evaporate with the water, so by law every home in Bermuda must collect 80% of the rain that falls on its roof.

Bermudan rooves are made of local limestone and channel rainwater into large underground tanks where the water is treated so that it can be used in homes. On average each Bermudan home can store about 50000 litres of water per bedroom.

Because Bermuda does not have a centralised water distribution system it also does not have a centralised sewage system and therefore has the highest density of private cesspits per square kilometre of anywhere in the world.

Do bowling balls float?

,

The largest bowling ball allowed by USBC or FIQ has a circumference of 27 inches, equivalent to a diameter of 21.9 centimetres and a volume of 5447 cubic centimetres. Whilst the size of a bowling ball is fixed, its weight can vary, typically between six and sixteen pounds (2.7 to 7.3 kilograms).

With a fixed volume and a changing mass the density (mass per unit volume) of a bowling ball will change, and as a result some bowling balls float, and some sink.

The low weight balls (including the 12 lb ball at a density of 999.6 kg/m3) all float. Only the 14 lb and 16 lb balls will sink.

The base rate fallacy

Imagine that there is a rare genetic disease that affects 1 in every 100 people at random. There is a test for this disease that has a 99% accuracy rate: of every 100 people tested it will give the correct answer to 99 of those people.

If you have the test, and the result of the test is positive, what is the chance that you have the disease?

If you think the answer is 99% then you are incorrect; this is because of the base rate fallacy – you have failed to take the base rate (of the disease) into account.

In this situation there are four possible outcomes:

Affected by disease Not affected by disease
Test correct Affected by disease, and test gives correct result. (DC) Not affected by disease, and test gives correct result. (NC)
Test incorrect Affected by disease, and test gives incorrect result. (DI) Not affected by disease, and test gives incorrect result. (NI)

This is easier to understand if we map the contents of the probability space using a tree diagram, as shown below.

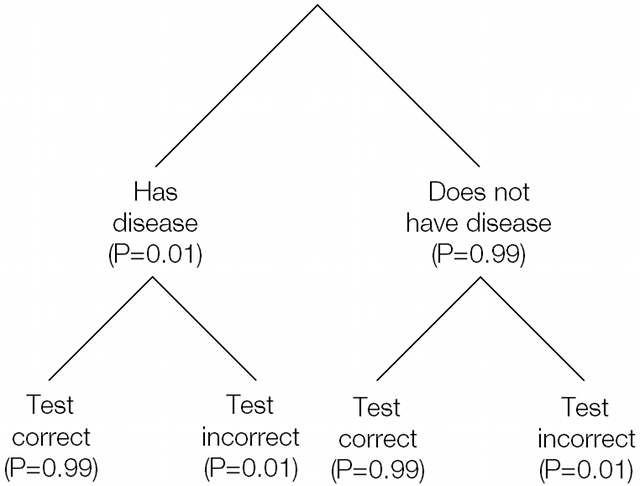
In two of these cases the result of the test is positive, but in only one of them do you have the disease.

P(DC) = P(Affected) × P(Test correct)
P(DC) = 0.01 × 0.99
P(DC) = 0.0099 = 1 in 101

The other case that results in a positive result, when you don’t have the disease and the test in incorrect has the same 1 in 101 probability: P(NI) = 0.0099.

Of the two remaining cases, not having the disease and getting a correct negative test result takes up the vast majority of the remaining probability space: P(NC) = 0.9801 or 1 in 1.02. The chance of having the disease and getting an incorrect test result is extremely small: P(DI) = 0.0001 or 1 in 10000.