Daily Archives: 20th August

The equation for the perfect bullshit equation

Every now and then a story appears in the media about how boffins (and it is always “boffins”) have worked out an equation for something: the perfect cup of tea, the most depressing day of the year, the best way to make pancakes, the perfect handshake, or in the most recent case, the perfect cheese on toast.

The Royal Society of Chemistry, whose boffins came up with the cheese on toast equation, really ought to know better, so to save any more of our august institutions from embarrassing themselves I have come up with an equation for the perfect bullshit marketing equation.

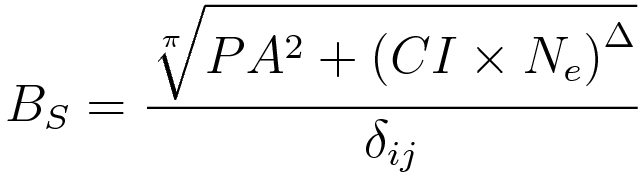
bullshit-equation-small

The equation for the perfect bullshit marketing equation
(rendered in \LaTeX to make it look more sciency).

B_{S} represents the amount of utter bullshit that this equation is. The subscript is there to make it look a bit more sciency.

PA^2 represents public appeal, which has no sensible unit, and is squared because most people remember the squared symbol from when they were at school and it looks really sciency without being too threatening. The PA term is also included because the P and A don’t kern properly for some reason and it will make graphic designers angry.

CI represents column inches, which has the unit of inches and is the only term with a unit, meaning that the final unit of utter bullshit is \textnormal{inches}^{\frac{\Delta}{\pi}} which is, as expected, utter bullshit. It and the PA term also represent the failure of bullshit equation-makers to understand that quantities in equations are only ever represented by individual symbols.

N_e represents Not Understanding What An Equation Is. The lowercase subscript e represents failing to take a consistent approach to the use of subscript in bullshit equations.

\Delta represents Not Understanding Dimensional Analysis. It’s an uppercase delta because that symbol already has a well-understood meaning and there is therefore no reason to use it but it looks sciency and hey, we’ve come this far, right?

The CI and N_e terms are multiplied together and added to the PA^2 term because any equation worth its salt has got to have some pluses and timeses in, otherwise it doesn’t even look like an equation.

The pi-th root of the PA^{2} + \left ( CI \times N_{e} \right )^{\Delta } term is used because by this stage it can’t make the equation any worse than it already is, nor any worse than any of the bullshit equations that have come before it.

\delta_{ij} is the Kronecker delta where i=4 and j=4 and is included because it looks really sciency whilst making absolutely no difference to the final result. The i and j terms were determined by rolling a die. I used the Kronecker delta rather than an Iverson bracket because I don’t really know what Iverson brackets are.

UPDATE: For how this post came about, check out this Storify story.

Lagrange points

,

In a system of two bodies, where one mass is much larger than the other (such as the Sun and Earth, or the Earth and Moon), there are five points, known as the Lagrange points, where the resultant gravitational field is such that it provides the centripetal force for that object to remain in constant orbit with those two bodies.*

What this means is that an object – such as a satellite – placed at a Lagrange point will remain at that point (relative to the two bodies) without need for any external force such as that provided by rocket or ion thrusters.

For example an object placed at point L1 in the diagram below will always remain between the Earth and the Sun and an object at L2 will always remain in the Earth’s shadow.

sun-earth-lagrange

The five Lagrange points of the Sun-Earth system. The white lines are gravitational contour lines: an object in free-fall would trace out a path along one of these contours.

L1

L1 is probably the easiest Lagrange point to understand. In the diagram above the Sun pulls towards the left, and the Earth pulls to the right, and the resultant force is just right to keep it in orbit between the Sun and Earth.

The L1 point is ideal for making observations of the Sun-Earth system as satellites placed here are never in the shadow of either the Sun or the Earth. The SOHO, ACE and WIND satellites are all positioned at L1.

L2

L2 is a good site for space-based observatories as it is almost perfectly protected from solar radiation and doesn’t receive any light pollution from Earth. The Planck telescope is currently at L2, the James Webb Space Telescope is scheduled to be placed there in 2018, and the WMAP and Herschel satellites were also previously positioned there.

L3

No satellites are currently positioned at L3, as it lies about 300 million kilometres from Earth. It has been suggested as a useful site for solar activity monitoring, as it would be able to spot any activity likely to affect Earth (sunspots, etc.) before the side of the Sun containing that activity was pointed towards Earth.

L3 is also popular in science fiction, as a place to “hide” something from Earth. After the development of interplanetary probes we checked and unfortunately there’s nothing there (yet).

L4 and L5

The L4 and L5 points lie at a 60° angle from the Sun-Earth axis, at the furthermost point of an equilateral triangle formed by the Sun and the Earth. Because this point is the same distance from both the Sun and Earth the ratio of their gravitational pulls is the same as if it were at the barycentre of the Sun-Earth system and objects placed there remain stationary. No satellites are currently placed at either point.

The Trojan asteroids are located at the L4 and L5 points of the Jupiter-Sun system. Asteroids are constantly being transferred between the asteroid belt and these two points.

* Lagrange points exist for any two-body system in which one object is much more massive than the other, but I’ll only be looking at the Sun-Earth system.