Imagine that there is a rare genetic disease that affects 1 in every 100 people at random. There is a test for this disease that has a 99% accuracy rate: of every 100 people tested it will give the correct answer to 99 of those people.
If you have the test, and the result of the test is positive, what is the chance that you have the disease?
If you think the answer is 99% then you are incorrect; this is because of the base rate fallacy – you have failed to take the base rate (of the disease) into account.
In this situation there are four possible outcomes:
| Affected by disease | Not affected by disease | |
| Test correct | Affected by disease, and test gives correct result. (DC) | Not affected by disease, and test gives correct result. (NC) |
| Test incorrect | Affected by disease, and test gives incorrect result. (DI) | Not affected by disease, and test gives incorrect result. (NI) |
This is easier to understand if we map the contents of the probability space using a tree diagram, as shown below.
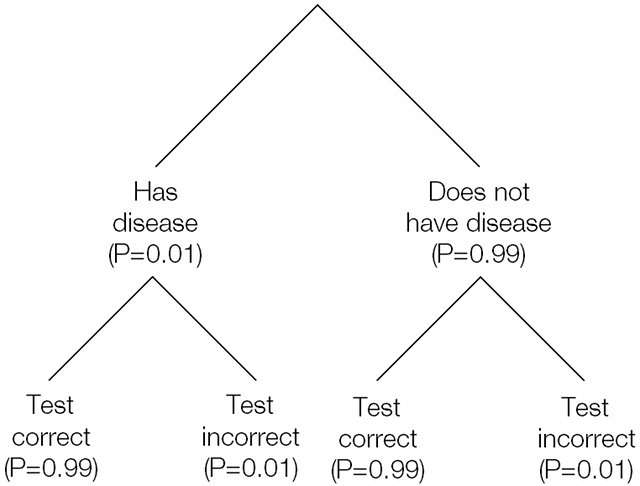
In two of these cases the result of the test is positive, but in only one of them do you have the disease.
P(DC) = P(Affected) × P(Test correct)
P(DC) = 0.01 × 0.99
P(DC) = 0.0099 = 1 in 101
The other case that results in a positive result, when you don’t have the disease and the test in incorrect has the same 1 in 101 probability: P(NI) = 0.0099.
Of the two remaining cases, not having the disease and getting a correct negative test result takes up the vast majority of the remaining probability space: P(NC) = 0.9801 or 1 in 1.02. The chance of having the disease and getting an incorrect test result is extremely small: P(DI) = 0.0001 or 1 in 10000.
Sorry but I’m afraid you’re wrong. Or rather, I think you mis-formulated the question. Your question should be: “if you take the test, what is the chance that the test results positive and you have the disease?”. As it is, it sounds like a fact that the test resulted positive, in which case its accuracy is 99%, and that’s the probability that you actually have the disease. I hope I’m making sense… :-)
Nope. I formulated the question in that way deliberately, otherwise the base rate fallacy doesn’t come in to play.
Hi . The post is a tad unclear. “If the result of the test is positive, what is the chance that you have the disease” – I get 50%. Rationale: Start with 10000 people. 100 have it and 99 test positive. Of the 9900, 99 will [ wrongly] come up as positive. So, if it is positive, the likelihood one really has the disease is (99 / [2*99]) = 50%.
I don’t think so. Of the 10000 people, 100 will have the disease and 99 of those will be correctly identified as having the disease. Of the remaining 9900 people, 99 will be incorrectly identified as having the disease. This makes 198 people of the 10000 who are identified as having the disease, but only half of those actually do have it and 99/10000 is 0.0099 as I stated in the post.
Stumbled upon your blog- its really great!
I have to concur with the second responder, tho. It’s 50%. That’s maybe not the answer to the question you think you asked, but it’s the answer to the question posed. You actually explained it perfectly in your last response. 99 w disease had positive test + 99 w/o disease w positive test = 198 w positive test. 99 w disease and positive test /198 w positive test =.50
Have to agree with Bela and Phil – the usual point of this example is the ‘not intuitive’ result that only 50% of those identified by the (99% accurate) test do in fact have the disease. Often this is portrayed as a very undesirable situation when
a) there is considerable anxiety associated with the possibility of having the disease and
b) the next step in the diagnosis work-up is invasive (painful and/or with the possibility of negative outcomes e.g. infection) , expensive or both. However, this combination is used so often that I fear that most students will think that it is never desirable to have a test that us only 99% accurate !
You have all made my point for me. Check your numbers again.
Yeah… I’m getting 50%…
“If you have the test, ***and the result of the test is positive***, what is the chance that you have the disease?”
So, “if the result of the test is positive” only applies to the 99 folks who have the disease and only the 99 folks who are false positives. This gets 50%.
You have fallen for the base rate fallacy. That is sort of the whole point of this article.
I think much of the confusion arises from the phrasing of the question.
If the question asked is: “What is the probability of having a positive test AND the disease?”, we take it that the anxious testee does not have information about whether his test is positive or negative. In that case, the probability in question is indeed 0.0099 as demonstrated in the original post.
However, how the original question is phrased, and what I believe is the more pertinent interpretation of the question is: “GIVEN that the result of the test is positive, what is the probability that the testee has the disease?”, where the fact that the result of the test is positive is known. The question then becomes a conditional probability problem.
P(Disease | Positive)
=P(Disease and Positive)/P(Positive)
=(0.1×0.99)/(0.0099×2)
=0.5
Which is less than the intuitive answer of 0.99 as it has taken into consideration the base rate of having the disease, 0.1, and therefore is NOT — base rate neglect.
That’s the point, Darren, yes.
I’ve never seen a more embarrassing admission of having made a mistake. You told everyone off for falling for the base rate fallacy until Darren managed to get through to you and you finally understood the answer really is 50%
And all you can say is, “That’s the point”?
You haven’t even corrected your question or answer. Maybe you managed to misunderstand Darren as well. Here’s an illustration. https://postimg.cc/N5ywxPhc
The essential non-intuitive aspect is that the great majority of healthy people result in that many more false positives to occur than false negatives.
I mean, nice try, Anthony, I guess? I absolutely 100% stand by everything I wrote orginally. It’s not my fault that you can’t understand that or the base-rate fallacy.