Tag Archives: astronomy

What is “Five Sigma” Data?

, , ,

or “Why do some experiments take such a long time to run?”

Before you go any further, watch the first minute of this video of Professor Andrei Linde learning from Assistant Professor Chao-Lin Kuo of the BICEP2 collaboration that his life’s work on inflationary theory has been shown by experiment to be correct.

The line we’re interested in is this one from Professor Kuo:

“It’s five sigma at point-two … Five sigma, clear as day, r of point-two”

You can see, from Linde’s reaction and the reaction of his wife, that this is good news.

The “r of point-two” (i.e. r = 0.2) bit is not the important thing here. It refers to the something called the tensor-to-scalar ratio, referred to as r, that measures the differences in the polarisation of the cosmic microwave background radiation caused by gravitational waves (the tensor component) and those caused by density waves (the scalar component).

The bit we’re interested in is the “five sigma” part. Scientific data, particularly in physics and particularly in particle physics and astronomy is often referred to as being “five sigma”, but what does this mean?

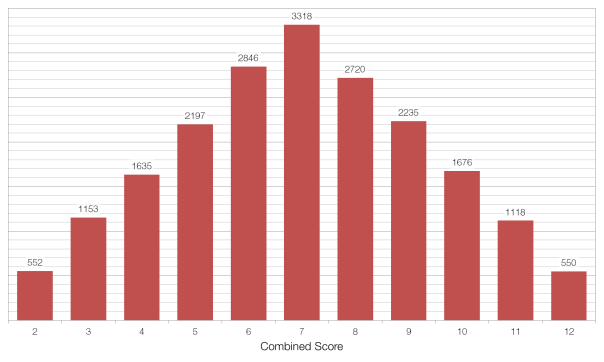
Imagine that we threw two non-biased six-sided dice twenty thousand times, adding the two scores together each time. We would expect to find that seven was the most common value, coming up one-sixth of the time (3333 times) and that two and twelve were the least common values, coming up one thirty-sixth of the time (556 times each). The average value of the two dice would be 7.00, and the standard deviation (the average distance between each value and the average) would be 2.42.

I ran this simulation in Microsoft Excel and obtained the data below. The average was 6.996 and the standard deviation (referred to as sigma or ?) was 2.42. This suggests that there is nothing wrong with my data, as the difference between my average and the expected average was only 0.004, or 0.00385 of a standard deviation, and this is equivalent to a 99.69% chance that our result is not a fluke, but rather just due to the expected random variation.

20000-throws-fair

Now imagine that we have a situation in which we think our dice are “loaded” – they always come up showing a six. If we repeated our 20000 throws with these dice the average value would obviously 12.0, which is out from our expected average by 5.00 or 2.07 standard deviations (2.07?). This would seem to be very good evidence that there is something very seriously wrong with our dice, but a 2.07? result isn’t good enough for physicists. At a confidence level of 2.07? there is still a 1.92%, or 1 in 52, chance that our result is a fluke.

In order to show that our result is definitely not a fluke, we need to collect more data. Throwing the same dice more times won’t help, because the roll of each pair is independent of the previous one, but throwing more dice will help.

If we threw twenty dice the same 20000 times then the expected average total score would be 70, and the standard deviation should be 7.64. If the dice were loaded then the actual average score would be 120, making our result out by 6.55?, which is equivalent to a chance of only 1 in 33.9 billion that our result was a fluke and that actually our dice are fair after all. Another way of thinking about this is that we’d have to carry out our experiment 33.9 billion times for the data we’ve obtained to show up just once by chance.

This is why it takes a very long time to carry out some experiments, like the search for the Higgs Boson or the recent BICEP2 experiment referenced above. When you’re dealing with something far more complex than a loaded die, where the “edge” is very small (BICEP2 looked for fluctuations of the order of one part in one hundred thousand) and there are many, many other variables to consider, it takes a very long time to collect enough data to show that your results are not a fluke.

The “gold standard” in physics is 5?, or a 1 in 3.5 million chance of a fluke, to declare something a discovery (which is why Linde’s wife in the video above blurts out “Discovery?” when hearing the news from Professor Kuo). In the case of the Higgs Boson there were “tantalising hints around 2- to 3-sigma” in November of 2011, but it wasn’t until July 2012 that they broke through the 5? barrier, thus “officially” discovering the Higgs Boson.

National Radio Quiet Zone

, ,

The US National Radio Quiet Zone (NRQZ) is a rectangle of land, approximately thirty-four thousand square kilometres in area, that crosses into Virginia, West Virginia and Maryland and contains the National Radio Astronomy Observatory at Green Bank and the Sugar Grove Research Facility at Sugar Grove (part of the US Navy’s Information Operations Command and said to be an important part of the NSA’s ECHELON system).

green-bank-telescope

The Green Bank Telescope, the world’s largest steerable radio telescope.

Within the NRQZ radio emissions are highly restricted; conventional television and radio  transmitters do not operates and people who (incorrectly) believe that they are sensitive to electromagnetic emissions have flocked there in order to deal with their “problem”. Electric fences, electric blankets, car electronics and even radio-tagged animals have all caused problems in the NRQZ and all on-site vehicles must have diesel engines rather than petrol engines, as diesel engines use the heat generated by compressing petrol vapour rather than spark plugs to ignite their fuel.

Cassiopeia

, ,

I am not really an astronomer or an astrophysicist (my expertise and interest is in the areas of nuclear and particle physics) but I will make an exception for the constellation of Cassiopeia.

The term “constellation” refers to a region of sky, so the constellation of Cassiopeia technically contains hundreds of stars, but what most people think of as Cassiopeia is the stretched ‘W’ shape made by the five brightest stars.

Alpha Cassiopeiae (α Cas, Schedar) is a cool (4500 K) orange giant star located 229 light-years from Earth. It is the brightest of the stars in Cassiopeia.

Beta Cassiopeiae (β Cas, Caph) is a warm (7100 K) yellow-white giant variable binary star 54.5 light-years from Earth. It is the second brightest of the stars in Cassiopeia and varies in apparent magnitude (brightness) between +2.25 to +2.31.

Gamma Cassiopeiae (γ Cas, Tsih) is a hot (31 000 K) blue subgiant eruptive variable binary star, the prototype of the shell type of variable stars. It is by far the most powerful of the stars in Cassiopeia but only the third brightest* as it is located 613 light-years from Earth. Gus Grissom, an astronaut who took part in Mercury and Gemini missions and who died in the Apollo 1 accident named the star “Navi”, after his middle name backwards, as the star was commonly used as a navigational aid during space missions.

Delta Cassiopeiae (δ Cas, Ruchbah) is a warm (8400 K) blue-white star, part of an eclipsing binary system. It is located 99.4 light-years from Earth.

Epsilon Cassiopeiae (ε Cas, Segin) is a hot (15 200 K) blue-white giant star and is the dimmest of the five, at a distance of 442 light-years from Earth.

Cassiopeia also contains some other interesting stuff: ρ Cassiopeiae and V509 Cassiopeiae are yellow hypergiants and two of the most luminous stars in the Milky Way, with ρ Cas being more than ninety million times the size of the Sun and around half a million times more powerful. Cassiopeia A is a the remnant of a supernova that occurred 300 years ago and the brightest source of radio waves outside of our own Sun. Cassiopeia also contains the Pacman nebula and two Messier objects, M52 and M103, both of which are open clusters visible from Earth with binoculars.

* The brightness of γ Cas varies irregularly but when it is at its brightest, with an apparent magntiude of +3.40, it is the brightest star in Cassiopeia.

Clockwise

,

Because the Earth rotates west to east, no matter where on Earth you are, the Sun rises in the east and sets in the west. In the northern hemisphere it passes through the south as it travels across the sky*, and in the southern hemisphere it passes through the north.

The first clocks that displayed the time (rather than measuring intervals of time) were simply sticks inserted vertically into the ground (gnomon). As the Sun moved across the sky the shadow cast by the stick would move across the ground; at midday the Sun would be at the south and the shadow would point north, to the “twelve o’clock” position.

An interesting consequence of this relates to the convention of “clockwise”:
If the development of the first clocks taken place in the southern hemisphere rather than in the northern hemisphere, clockwise and anticlockwise would be in opposite directions.

* Hence why, in the northern hemisphere, a south-facing garden is an attractive selling point for a house.