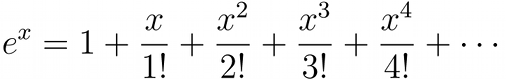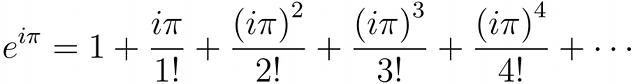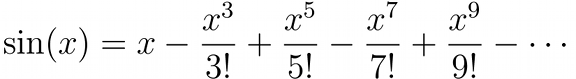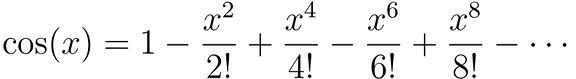Computer designed camouflage

,

In 1996 Canada became the first country to adopt battledress with a camouflage pattern generated by a computer, also known as digital camouflage.

L-R: Simulated CADPAT (Canadian Disruptive Pattern) for temperate, arid and arctic regions.

It is not the pixellated appearance of the pattern from which digital camouflage gets its name. There are a number of pixellated patterns that are not digital camouflage (e.g. Soviet “Birch Leaf”), and a number of digital camouflage patterns that are not pixellated (e.g. Italian “Vegetato”).

Rather the term “digital camouflage” comes from the computer-aided process by which the pattern is developed, using computer models of how human vision works and applying complicated computer techniques such as fractal generation and recursive algorithms employing both macro- and micro-patterns. The hope is that this more scientific approach will result in camouflage patterns with lower detectability, and this seems borne out by the fact that most militaries are now adapting digital camouflage patterns.

Salt flats and giant space mirrors

, ,

A salt flat is formed when a pool of salt water evaporates, depositing salt as it does. This layer of salt builds up over time and seasonal flooding causes a very flat surface to form.

Salar de Uyuni in Bolivia, the largest salt flat in the world.

When covered in water, salt flats become the largest mirrors in the world.

Salt flats are commonly used to calibrate observation satellites, as they provide very large and flat areas (Salar de Uyuni has an area of more than 10 000 square kilometres and varies in height by less than one metre). The surface of salt flats are highly reflective and because they occur in desert areas there is usually very little cloud cover and very clear air.

Understanding Euler’s Identity


Euler’s Identity, shown above, is often said to be the most beautiful equation in all of science and mathematics.

It links the three basic arithmetic operations:

  • Addition, in the +1 term.
  • Multiplication, in the iπ term.
  • Exponentiation, in the eiπ term.

It also links five of the most important mathematical constants:

  • e, the base of the natural logarithms.
  • i, the imaginary number (√−1) on which complex numbers are based.
  • π, the ratio of a circle’s circumference to its diameter.
  • 1, the multiplicative identity, the basic unit of counting.
  • 0, the additive identity that leaves a number unchanged.

Understanding how eiπ + 1 can equal zero is more difficult.

To begin to understand how to evaluate Euler’s Identity we must first understand about series expansions. The series expansion of a function can be used to calculate the value of this function to an arbitrary degree of precision.

The series expansion of ex is given by:

If only the first term is used then e = 1.00, if two terms are used e = 2.00, if three terms are used e = 2.50, if four terms are used e = 2.66, and so on, until an infinite number of terms are used and the exact value of e is given. After only ten terms the value found for e is accurate to better than one part in a million.

The series expansion of eiπ is therefore given by:

The even powered terms (e.g. i2π2, i4π4) become negative because i2=−1 and the odd powered terms (e.g. i3π3, i5π5) gain a negative multiple of i.

There are two other important expansions, the expansion of sin(x) and cos(x), two basic trigonometric functions.

If we collect the terms in the expansions of sin(x) and cos(x) and compare them with the expansion of eix we find that:

Inserting π in place of x in that expression yields:

Because cos(π) = −1 and sin(π) = 0 we find that indeed, eiπ = −1 and therefore eiπ + 1 = 0.