Telomeres

,

A telomere is a section of repetitive DNA* found at the end of the chromatids that make up a chromosome. Unlike normal DNA, telomeres do not code for the production of proteins – they are non-coding DNA. The purpose of telomeres is to protect the important coding DNA during the DNA copying process; without telomeres the ends of each chromatid would be lost during cell division. Dr Elizabeth Blackburn, who won the 2009 Nobel Prize in Medicine or Physiology for her work on telomeres likened them to the plastic caps on the ends of shoelaces that prevent them from fraying.

telomeres

Human chromosomes with telomeres highlighted in yellow.

Imagine that cell division works like photocopying, with each division making a perfect photocopy of the original. However, this photocopier is not perfect, and always loses the last five pages in the copying process, making the copy five pages shorter than the original. Adding telomeres to the end of chromatids is like adding many blank pages to the end of your original before the copying process starts. Although five pages are lost during each copy, there are many, many blank pages that can afford to be lost before important (i.e. coding DNA) pages begin to be lost.

During the aging process telomeres become shorter and shorter, and the shorter your telomeres are the more susceptible you are to disease and the shorter your lifespan is likely to be.

* In humans telomeres code the sequence “TTAGGG” over and over again.

Chrysopoeia

,

Chrysopoeia is the artificial production of gold, long the goal of alchemists (particularly the transmutation of base metals, such as lead). Turning one element into another via chemical reactions is impossible, but it is possible using nuclear reactions.

Gold-crystals

Crystalline gold

Gold has only one stable isotope, gold-197, so any nuclear reaction aiming to produce gold must finish with producing gold-197. If your reaction produces another gold isotope, such as gold-196 or gold-198 this will decay over the course of a few days to form another element (platinum-196 or mercury-196 in the case of gold-196, and mercury-198 in the case of gold-198).

Producing gold from lead is impossible, but it is possible to turn mercury into gold. If mercury-196 (0.15% of natural mercury) is irradiated with slow neutrons it forms mercury-197 which then decays via electron capture to form stable gold-197. If mercury-198 (9.97% of natural mercury) is used instead, it can be irradiated with fast neutrons, causing it to lose a neutron and form mercury-197 and then gold-197 as above.

In 1980 Glenn Seaborg (after whom seaborgium is named) produced a tiny amount of gold (thousands of atoms) by bombarding bismuth-209 with carbon-12 and neon-20 atoms, but only formed radioactive isotopes of gold in the process.

Regardless of the method used, the production of gold in nuclear reactions is prohibitively expensive, costing many times the price of gold per unit mass produced.

Averages

An average is way of expressing, in a single figure, important information about a population.

The arithmetic mean is probably what you think of when you think of average. To find the arithmetic mean you sum all the values in your set, and then divide by the number of values. So the arithmetic mean of 1, 1, 2, 3, 5, and 8 is 20/6 or 3⅓.

The median is the middle value within a set when the set is arranged in order. So the median of 1, 1, 2, 3, 5, 8, 13 is 3, because 3 is the fourth value in a set of seven values. If the number of values in the set is even, then the median is half-way between the two middle values. Therefore the median of  1, 1, 2, 3, 5, 8 is 2.5, because 2 and 3 are the third and fourth value in a set of six values.

The median is useful when your data contains outliers. For example, in a class of ten pupils who score 91%, 92%, 93%, 94%, 95%, 96%, 96%, 98%, 99% and 10% the arithmetic mean average is 86.5%. Does this seem correct? Would it be correct to report this as the class’s “average mark”? In this situation it’s more sensible to report the median mark, which in this case is 95.5%.

The median is the most resistant average – it takes a great deal of contamination (e.g. by outlier values) to cause it to breakdown and give an arbitrarily large or small value. To corrupt the median value, more than 50% of the data have to be “contaminated”, in which case your data-collection process is probably fundamentally flawed.

The mode is the most common value within a set. So the mode of 1, 1, 2, 3, 5, 8 is 1, because 1 appears twice and the rest of the numbers only appear once. The mode is the only average that makes sense when dealing with non-numerical data: the mode eye colour (brown in the UK), or the mode surname (Smith in the UK), for example.

The geometric mean is useful when you are comparing values that have different ranges. For example, take the two computers specified below:

CompuTron 9001 Comp-O-Matic A1
Clock Speed /GHz 4.00 4.50
RAM /GB 4.00 8.00
Hard Disk /GB 1250 1000
Arithmetic Mean 419 338
Geometric Mean 27.1 33.0

The CompuTron 9001 scores higher on the arithmetic mean because the size of the hard disk has a disproportionate effect (it is of the order of 103, whereas the clock speed and RAM values are of the order of 100), but the geometric mean shows that the Comp-O-Matic A1 is better overall.

The geometric mean of a set of n values is the nth-root of the product of the values in the set, or in algebraic terms:

\bar{x}_{GM}=\left(\prod_{i=1}^n{x_i}\right)^{\frac{1}{n}}

The geometric mean is also useful when your data has a very large range. For example, if we looked at the gross domestic product (GDP) of ten countries picked at random we might end up with the data shown below:

Country GDP /$bn Country GDP /$bn
Slovenia 50.3 Spain 1480
Niger 6.38 Ukraine 165
USA 15000 Bermuda 5.97
Albania 13.0 Jordan 28.8
Monaco 5.92 Croatia 62.5

Here the largest value (USA) is more than two-and-a-half thousand times larger than the smallest value (Monaco). Is it fair to say that the “average” GDP for countries in this list is the arithmetic mean of $1680 billion, when nine out of the ten countries in the list have a GDP less than this, and seven of the ten have a GDP less than one-tenth of this? For these countries the geometric mean of $62.9 billion might be a better choice. (The median is probably not a good choice as we have a very limited data set with a long tail.)

The harmonic mean is especially important in physics, particularly when dealing with rates (e.g. speed, acceleration) and ratios (e.g. resistance, capacitance). If a car drives 100 kilometres one way at 60 km/h and then back the same distance at 40 km/h you would be forgiven for thinking that its “average” speed is 50 km/h. However, this is not true as it doesn’t take account of the fact that the car spends more time at 40 km/h than it does at 60 km/h.

Calculating the harmonic mean of these two speeds using the equation below yields the correct average speed of 48 km/h.

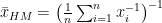
\bar{x}_{HM}=\left(\frac{1}{n}\sum_{i=1}^n x_{i}^{-1}\right)^{-1}

The same is true when considering fuel economy: the average miles per gallon figure for two cars, one 30 mpg and one 50 mpg driving the same distance is not 40 mpg but rather the harmonic mean of the two figures, 37.5 mpg.

In a network of n resistors in parallel, or n capacitors in series, the harmonic mean of the resistors’ or capacitors’ values yields the correct average value of each resistor’s or capacitor’s contribution to the network. For example: a 90Ω and 10Ω resistor in parallel have a combined resistance of 9Ω. The harmonic mean of 90Ω and 10Ω is 18Ω, and two 18Ω resistors in parallel yield a total resistance of 9Ω. (If the resistors are in series, or the capacitors in parallel, then the arithmetic mean should be used.)

The weighted mean is similar to the arithmetic mean, but takes account of the relative contributions of each component. Consider the data below:

Subject Number of Students Pass Rate
Science 100 100%
English 400 50%
Mathematics 400 50%

A naïve Headteacher might simply take the average of 100%, 50% and 50% and claim that the overall pass rate was 68%. However, this fails to take account of the fact that far more students were studying English and Maths than were studying Science, and so the correct average pass rate was 56%.

There is not necessarily a “correct” average to use for any given situation. You should base your choice of average on trying to fulfil the criterion at the top of this post: a single number that best represents the entire set of data.

Subject-Verb-Object

Sentences have three main parts: the subject of the sentence, the object of the sentence, and a verb that links the two together.

In English, sentences follow the SVO (subject-verb-object) order, for example in the sentence “She loves him”, “She” is the subject, “loves” is the verb and “him” is the object. Other languages that follow the SVO order include Chinese, French and Russian, but SVO is not the most common arrangement.

The most common arrangement is SOV (subject-object-verb), which is found in 45% of languages (as opposed to the 42% of languages which use SVO) and in this case, our example sentence becomes “She him loves”. This arrangement is found in Japanese, Korean and Pashto.

The remaining 13% of languages use the other four possible arrangements:

  • VSO (“Loves she him”) is found in 9% of languages, including Arabic, Hebrew and Gaelic. (i.e. it is found in the semitic and celtic languages.
  • VOS (“Loves him she”) is found in 3% of languages, including Malagasy, Tagalog and Fijian.
  • OVS (“Him loves she”) and OSV (“Him she loves”) make up the remaining 1% of languages, with OSV being present in only one known case: Warao, spoken by around 28 000 people in Venezuela, Guyana and Suriname.

Just because a sentence doesn’t follow the SOV arrangement doesn’t mean that it won’t be understandable to English speakers. One of the most famous sentences in the English language “With this ring, I thee wed.” follows the SOV arrangement.

Where did all the elements come from?

Matter is made up of atoms, and each atom is one of (currently) 118 elements. But where did those elements come from?

Note: Each element has a different atomic number (represented by the symbol Z (from the German Zahl for number) which represents the number of protons in the element’s nucleus.

Hydrogen, Helium and Lithium (Z=1 to Z=3)

Hydrogen, helium and lithium were formed in the Big Bang, by a process called Big Bang nucleosynthesis. Unstable radioactive isotopes of beryllium were also formed, but those would quickly decay into other elements or fuse with other stable atoms.

Big Bang nucleosynthesis occurred from about one-tenth of a second to one thousand seconds after the Big Bang and involved the creation of protons and neutrons from the quark-gluon plasma that existed before it, and then the creation of hydrogen, helium and lithium from these protons and neutrons.

Beryllium to Iron (Z=4 to Z=26)

A process called stellar nucleosynthesis, where lighter elements are fused into heavier ones with the release of energy (i.e. an exothermic fusion reaction) is responsible for the creation of the elements from beryllium to nickel. Some nickel-56 and zinc-60 is also produced, but these are unstable and decay quickly to form iron-56 and copper-60. It is the decay of nickel-56 into iron-56 which is responsible for the high amount of iron-56 found in meteorites and planetary cores. (For example, both the Earth’s solid inner core and liquid outer core are composed primarily of an iron-nickel alloy.)

There are a variety of stellar nucleosynthesis processes responsible for the formation of these elements: the alpha and triple-alpha processes and the “burning” of lithium, carbon, neon, oxygen and silicon formed in earlier stages. Stellar nucleosynthesis is also responsible for the creation of more helium via the “burning” of deuterium, the proton-proton chain, and the carbon-nitrogen-oxygen cycle.

Cobalt to Californium (Z=27 to Z=98)

There are three processes responsible for the creation of elements heavier than iron: the S-process, the R-process and the Rp-process (sometimes called the P-process). The S-process (slow neutron capture) occurs in low- to medium-mass stars and is when neutrons emitted by fusion reactions between lighter elements are absorbed by heavy nuclei like iron; this process forms about half of the elements heavier than iron.

The R-process (rapid neutron capture) probably occurs in the core of core-collapse supernovae when electrons are forced back “inside” protons to produce an extremely high flux of neutrons which are rapidly absorbed (hence the name) by heavy nuclei like iron. The R-process forms about half of the elements heavier than iron, and most if not all of the heaviest elements like uranium.

A minority of the heavier elements are formed by the Rp-process (rapid proton capture), and these are all lighter elements (evidence suggests it cannot form elements heavier than tellurium (Z=52). It occurs in very high-temperature hydrogen-rich environments like the outer layers of a star undergoing a core-collapse supernova.

Trace amounts of heavier-than-iron elements with atomic numbers 92 to 99 were, and are, also produced naturally on Earth by radioactive decay processes.

Einsteinium to Ununoctium (Z=99 to Z=118)

Small amounts of the lightest of these elements may be produced as outlined above by the S-, R- and Rp-processes, but the majority of them have only ever been produced artificially, in laboratories, by humans. They are all extremely radioactive and have very short half-lives so only exist for tiny fractions of a second when they are created (e.g. element 118, ununoctium has a half life of about 0.9 milliseconds).

The processes by which these heaviest of the elements are created vary. Einsteinium was first detected as a by-product of the first fusion bomb (H-bomb) test, fermium is formed by bombarding lighter lanthanides with neutrons, and mendelevium by the bombardment of californium by alpha particles. The remaining elements have all been created by smashing together two larger nuclei: for example, ununoctium was first produced by colliding krypton-86 and lead-208.