Types of Perpetual Motion Machines

Perpetual motion machines (which don’t exist) come in many forms.

Perpetual motion machines of the first kind violate the First Law of Thermodynamics. They produce mechanical work (i.e. movement) without any energy being input; this violates the principle of the conservation of energy.

Perpetual motion machines of the second kind violate the Second Law of Thermodynamics. They convert thermal energy directly into mechanical work, with no exhaust heat being emitted; this violates the rule of the production of entropy, that entropy in a system must always increase.

Perpetual motion machines of the third kind do not, as their name suggests, violate the Third Law of Thermodynamics. Rather they claim to maintain motion (once started) forever, and do so by assuming that frictional forces can be eliminated completely (often through operating in a perfect vacuum, which is also not possible).

 

Altitude and Flight Level

,

The term elevation refers to the position of a point or an object on the ground above a fixed reference point, usually mean sea level. The term altitude refers to the position of a point or object in the air above a fixed reference point.

But defining altitude can be difficult, and so when altitude is referred to, the reference point must always be explicitly defined. Altitude is normally measured above mean sea level (AMSL) or above ground level (AGL). For example, if an aeroplane flew over the peak of Mount Everest, its altitude could be referred to as either 38 000 ft AMSL or 9000 ft AGL, because the peak of Everest has an elevation of 29 000 ft.

For aircraft it is difficult to measure altitude. You might think that GPS could provide this information, but GPS is designed for positioning on the surface of the Earth and isn’t very good at measuring altitude.

Pilots have always used atmospheric pressure to measure altitude. As an aircraft moves further upwards into the air, there is less air above it pushing down on it and the pressure decreases. This decrease is predictable and easy to calculate:

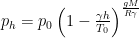
p_h = p_0 \left( 1- \frac{\gamma h}{T_0} \right)^{\frac{gM}{R\gamma}}

where 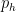p_h is the pressure at height 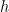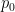h; p_0 is the standard atmospheric pressure of 1013.25 hPa; 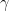\gamma is the rate at which temperature decreases with altitude (the temperature lapse rate); 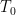T_0 is the standard temperature; 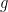g is the gravitational field strength; 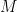M is the molar mass of dry air; and 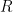R is the molar gas constant.

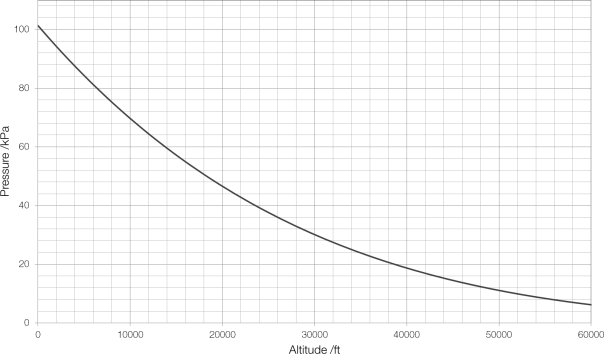
altitude-pressure

Aeroplanes do not fly at a set altitude. Rather they fly at a given flight level, which – although it sounds like a height – is actually a pressure. When a pilot flies at a flight level of 32 000 ft (FL320) they are actually flying at a constant pressure of 275 hPa, and may actually be far above or far below this altitude, depending on the local weather (and therefore pressure) conditions. If they enter an area of particularly high or low pressure they will have to ascend or descend correspondingly.

Using flight levels helps to prevent collisions between aircraft: in the UK aircraft flying on headings between 000° and 089° (north to east) they flight at odd numbered flight levels (FL310, FL330, etc); flying between 090° and 179° (east to south) at odd numbered flight levels plus 500 ft (FL315, FL335); flying between 180° and 269° (south to west) at even numbered flight levels (FL320, FL340); and flying between 270° and 359° (west to north) at even numbered flight levels plus 500 ft (FL325, FL 345). In other parts of the world different flight level rules are used.

2014-2015 Review

Mr Reid travelling salesman problem (2000 nodes)

I had a very busy timetable at work this year, so I didn’t blog here as much as I would have liked. Hopefully the 2015-2016 Review will be longer than this one.

I enjoyed writing about rotational kinetic energy in September, and the difference between centre of mass and centre of gravity was something people don’t often think about.

A post on how latitude affects the length of the day was my favourite post from October.

November was one of my favourite months: I particularly liked the posts about fail-safes, citrus fruit and analemmas.

I only made two posts in December, about the colour of diamonds and the possibility of building a vacuum airship, but I liked them both.

January was also a good month. My favourites were two posts about ranking things properly, and the different types of microscope. I also wrote about different naming systems across the world, but I’m not sure I got my facts 100% correct.

A post about the thermal expansion of petrol was easily my favourite post from February.

I liked all the posts I made in March, particularly the posts about colour mixing (why is light red, green and blue, but ink cyan, magenta and yellow?), the order of adjectives in English, and alternatives to GPS.

April was also a good month: I wrote about the nuclear “double flash” and worked out a much better system of coinage for the UK.

A post about how to look at the back of your head using a black hole was my favourite post from May.

I didn’t make any posts in June. :(

I particularly like my post about why some particles don’t decay from July. I also wrote about the different type of multiplication and the world’s longest golf shot.

August was another good month (school holidays!). I wrote about the US’s “soft bomb”, longitude, latitude and precision and the Kp index for aurora spotting.

Here’s to 2015-2016. I hope you’ll keep reading.

Soft Bomb

A soft bomb (also known as a “blackout bomb”) is a bomb designed to destroy electrical power infrastructure rather than physical buildings. The only known soft bomb is the US’s CBU-94 cluster bomb dispenser carrying BLU-114/B warheads (the finer details of which are still classified).

Once dropped by an aircraft, as it is falling, the bomb orients itself vertically and then discards its outer casing and begins spinning. Once it is spinning it releases two hundred drink can-sized submunitions, each of which contains thousands of tiny graphite fibres. A small explosive charge inside each submunition then detonates, scattering the graphite fibres like electrically conducting confetti and forming a “net” that drifts slowly downwards. When this conductive confetti lands on the target – an electrical transformer or substation – it causes thousands of explosive short circuits, starting fires and disabling the target.

blu-114

Soft bombs was first used in May 1999, as part of US operations in Serbia, in which night-time strikes by F-117A stealth fighters knocked out electricity to 70% of the country. They were then used again a few days later to undo repairs that the Serbians had completed. The photograph above comes from a video shot at the TPP Nikola Tesla power plant that was heavily damaged in the attack.

Longitude, Latitude and Precision

,

There are two main ways of giving longitude and latitude: in degrees, minutes and seconds, and in decimal degrees. For example: the current headquarters of the Institute of Physics could be given as 51° 31′ 18.0721″N, 0° 8′ 42.8759″W in degrees, minutes and seconds format; or as 51.521687, -0.145243 in decimal degrees. (Note the absence of cardinal directions in the decimal degrees format: positive latitude values are taken to be north, with negative values being south, and positive longitude values taken to be east, and negative values west.)

Lines of longitude are great circles, each one the same size, running around the Earth and crossing both the north and south poles. When quoting the position of an object on Earth’s surface in terms of its longitude, the degree of precision is not affected by the longitude in question.

Precision Error
1.0° / 1.0° 0′ 0″ ± 111 km
0.1° ± 11.1 km
0° 1′ 0″ ± 1.85 km
0.01° ± 1.11 km
0.001° ± 111 m
0° 0′ 1″ ± 30.9 m
0.0001° ± 11.1 m
0.00001° ± 1.11 m
0.000001° ± 0.111 m

Unlike lines of longitude, not all lines of latitude are the same length. At 80° latitude the length of the line of latitude is only 17.3% of that at the equator. This means that the level of precision changes with latitude – each division of the latitude line is much smaller at you approach the north pole.

latitude-precision

As you can see in the graph above, the change is not linear with latitude. The same 35° difference in latitude yields very different results in terms of accuracy.

This means that different locations will need to use different degrees of accuracy in their GPS coordinates if you want people to be able to find their way around. At Quito, near the equator at 0.23°N, a precision of 0.001° would lead to an accuracy of ± 111 metres, but at Helsinki, much further north at 60.2°N, this accuracy is improved to ± 55 metres.